In our work, we often discuss the fundamental flaws in modern networking--protocols built on the "Minkowski fallacy" of smooth, universal time, leading to "data corruption" and "silent data loss" because they lack a true mechanism for "perfect information feedback".
Our alternative begins with a different physical and logical foundation: a mesh of nodes, a "sea of XPUs", engineered for "temporal intimacy". In this environment, the network must be self-discovering. Before you can route, you must scout.
These concepts can seem abstract. As our colleague Dugan Hammock has demonstrated a powerful tool for making these ideas concrete, this article uses the Wolfram Language to model and analyze the principles of "discovery and pathfinding for a mesh-based network", including its behavior in the face of the inevitable failures that all real-world systems must endure.
Building the Lattice: A Model for "Temporal Intimacy"
First, we define our network. We use an octagonal lattice, a highly-connected 8-neighbor mesh. This grid represents our "Distributed Autonomous Ethernet (DAE)" rack, where nodes are physically close. The code defines the precise positions of each node and, crucially, the adjacencyList--the best of the map, of all "bidirectionally coherent" links that form the basis of our network.
ClearAll["Global`*"];
Unprotect[$PerformanceGoal];
$PerformanceGoal = "Quality";
Protect[$PerformanceGoal];
rows = 11;
cols = 11;
r = 1;
gap = 0.2;
dx = 2 r (Cos[\[Pi]/8] + gap);
dy = 2 r (Cos[\[Pi]/8] + gap);
OctagonAt[{x_, y_}, rr_] :=
Polygon[Table[{x, y} +
rr RotationTransform[\[Pi]/8 + (i \[Pi])/4][{1, 0}], {i, 0, 7}]];
positions =
Association[
Flatten[Table[
With[{id = j cols + i + 1}, id -> {i dx, j dy}], {j, 0,
rows - 1}, {i, 0, cols - 1}], 1]];
adjacencyList =
Association[
Flatten[Table[
Module[{id, neighbors, validNeighbors}, id = j cols + i + 1;
neighbors = {{i - 1, j}, {i + 1, j}, {i, j - 1}, {i,
j + 1}, {i - 1, j - 1}, {i + 1, j - 1}, {i - 1,
j + 1}, {i + 1, j + 1}};
validNeighbors =
Select[neighbors, 0 <= #1[[1]] < cols && 0 <= #1[[2]] < rows &];
id -> (#2 cols + #1 + 1 &) @@@ validNeighbors], {j, 0,
rows - 1}, {i, 0, cols - 1}], 1]];
centerI = 0;
centerJ = 0;
rootNode = centerJ cols + centerI + 1;
Print["Root node (center position: ", {centerI, centerJ},
") with valency: ", Length[adjacencyList[rootNode]]];
BFS[root_, adjList_] :=
Module[{distances, queue, current, neighbors},
distances = Association[root -> 0]; queue = {root};
While[Length[queue] > 0, current = First[queue];
queue = Rest[queue]; neighbors = adjList[current];
Do[If[! KeyExistsQ[distances, neighbor],
distances[neighbor] = distances[current] + 1;
AppendTo[queue, neighbor];], {neighbor, neighbors}];];
distances];
distances = BFS[rootNode, adjacencyList];
GetAccessibleLinksUpToHop[maxHop_] :=
Module[{accessibleLinks = {}, linkPair, uDist, vDist},
Do[Do[linkPair = Sort[{node, neighbor}];
If[! MemberQ[accessibleLinks, linkPair], uDist = distances[node];
vDist = distances[neighbor];
If[uDist <= maxHop && vDist <= maxHop &&
Min[uDist, vDist] <= maxHop - 1,
AppendTo[accessibleLinks, linkPair];];], {neighbor,
adjacencyList[node]}], {node, Keys[adjacencyList]}];
accessibleLinks];
maxHop = Max[Values[distances]];
hopCounts = Table[Count[Values[distances], h], {h, 0, maxHop}];
cumulativeNodeCounts =
Table[Count[Values[distances], x_ /; x <= h], {h, 0, maxHop}];
linkCountsAtHop =
Table[Module[{currentLinks, previousLinks},
currentLinks = GetAccessibleLinksUpToHop[h];
previousLinks = If[h > 0, GetAccessibleLinksUpToHop[h - 1], {}];
Length[currentLinks] - Length[previousLinks]], {h, 0, maxHop}];
cumulativeLinkCounts =
Table[Length[GetAccessibleLinksUpToHop[h]], {h, 0, maxHop}];
Print["Hop counts (nodes): ", hopCounts];
Print["Cumulative accessible nodes: ", cumulativeNodeCounts];
Print["New link counts at each hop: ", linkCountsAtHop];
Print["Cumulative accessible links: ", cumulativeLinkCounts];
Print["Links at hop 0: ", Length[GetAccessibleLinksUpToHop[0]]];
Print["Links at hop 1: ", Length[GetAccessibleLinksUpToHop[1]]];
edgeToNodePair =
Union[Sort /@
Flatten[Table[
Table[{id, neighbor}, {neighbor, adjacencyList[id]}], {id,
Keys[adjacencyList]}], 1]];
edges = (Line[{positions[#1], positions[#2]}] &) @@@ edgeToNodePair;
Print["Sample edge node pairs: ", Take[edgeToNodePair, UpTo[5]]];
hopColor[hop_] := ColorData["BrightBands"][Rescale[hop, {0, maxHop}]];
gridBackground = White;
plotBackground = White;
frameStyle = Directive[Black, Thick];
labelStyle = Directive[Black, 14, Bold];
subtitleStyle = Directive[GrayLevel[0.2], 11];
maxCount = 1.1 Max[Join[cumulativeNodeCounts, cumulativeLinkCounts]];
CreateGridFrame[currentHop_] :=
Module[{accessibleNodes, accessibleLinkPairs, linkGraphics,
nodeGraphics, activeLinkCount, xRange, yRange},
accessibleNodes =
Select[Keys[distances], distances[#1] <= currentHop &];
accessibleLinkPairs = GetAccessibleLinksUpToHop[currentHop];
linkGraphics =
Function[pair,
If[MemberQ[accessibleLinkPairs, pair],
Module[{avgHop = Mean[distances /@ pair], c},
c = hopColor[avgHop]; {Directive[Thickness[0.006], Glow[White],
c], Line[{positions[pair[[1]]],
positions[pair[[2]]]}]}], {Directive[GrayLevel[0.6], Thin,
Opacity[0.4]],
Line[{positions[pair[[1]]], positions[pair[[2]]]}]}]] /@
edgeToNodePair; activeLinkCount = Length[accessibleLinkPairs];
nodeGraphics =
Table[Module[{nodeHop, color}, nodeHop = distances[node];
color = If[nodeHop <= currentHop, hopColor[nodeHop],
Directive[GrayLevel[0.8], Opacity[0.5]]]; {EdgeForm[{Black,
Thickness[0.003]}], FaceForm[color],
OctagonAt[positions[node], r]}], {node, Keys[positions]}];
xRange = {Min[Values[positions][[All, 1]]] - 1.5,
Max[Values[positions][[All, 1]]] + 1.5};
yRange = {Min[Values[positions][[All, 2]]] - 1.5,
Max[Values[positions][[All, 2]]] + 1.5};
Column[{Style[
Row[{"Hop: ", currentHop, " \[Bullet] Accessible Nodes: ",
Length[accessibleNodes], " \[Bullet] Accessible Links: ",
cumulativeLinkCounts[[currentHop + 1]],
" \[Bullet] Active Links (this hop): ", activeLinkCount}],
subtitleStyle],
Graphics[{{Opacity[0.15, White], Thick, EdgeForm[],
Disk[Mean[Values[positions]], 2 Max[dx, dy] {rows, cols}]},
linkGraphics, nodeGraphics}, ImageSize -> 450,
Background -> gridBackground, PlotRange -> {xRange, yRange},
PlotRangePadding -> Scaled[0.05], ImagePadding -> 25]}]];
CreateNodeGraphFrame[currentHop_] :=
Module[{currentCumulativeNodes, currentCumulativeLinks, hops},
hops = Range[0, currentHop];
currentCumulativeNodes = cumulativeNodeCounts[[1 ;; currentHop + 1]];
currentCumulativeLinks =
cumulativeLinkCounts[[1 ;; currentHop + 1]];
ListLinePlot[{Transpose[{hops, currentCumulativeLinks}],
Transpose[{hops, currentCumulativeNodes}]},
PlotStyle -> {Directive[Thick, ColorData["BrightBands"][0.85]],
Directive[Thick, Dashed, ColorData["BrightBands"][0.25]]},
Filling -> {1 -> Axis},
FillingStyle ->
Directive[Opacity[0.25], ColorData["BrightBands"][0.7]],
PlotRange -> {{0, maxHop}, {0, maxCount}}, Frame -> True,
FrameStyle -> frameStyle, FrameTicksStyle -> Directive[Black, 10],
Axes -> False,
PlotLegends ->
Placed[{Style["Cumulative accessible links", 11, Black],
Style["Cumulative accessible nodes", 11, Black]}, {0.02, 0.95}],
GridLines -> {Range[0, maxHop, 1], Automatic},
GridLinesStyle -> Directive[GrayLevel[0.8, 0.7], Dashed],
ImageSize -> 450, Background -> plotBackground,
PlotLabel ->
Style["Node & Link Accessibility vs Hop Count", labelStyle],
AxesLabel -> {Style["Hop Count", 11, Black],
Style["Count", 11, Black]}, ImagePadding -> {{50, 15}, {45, 25}}]];
animation =
Animate[Column[{Row[{CreateGridFrame[h], Spacer[30],
CreateNodeGraphFrame[h]}, Alignment -> Center]},
Spacings -> 2], {h, 0, maxHop, 1}, AnimationRate -> 1,
AnimationDirection -> Forward, AnimationRepetitions -> \[Infinity]];
frames =
Table[Row[{CreateGridFrame[h], Spacer[30], CreateNodeGraphFrame[h]},
ImageSize -> 950, Alignment -> Center], {h, 0, maxHop}];
ListAnimate[frames];
Export["hopLinks_beautiful.gif", frames, "DisplayDurations" -> 1];
animation
Scouting the Network: The Breadth-First Search (BFS)
With the lattice defined, we need a "scouting" protocol. We start with a foundational algorithm: a Breath-First Search (BFS). This allows a rootNode (here, one chosen near the corner) to discover its environment, calculating the hop-count (distance) to every other node it can reach. And, these bricks that let us build further and further can flood back in the form of a recursive map of distances that, is the fundamental prerequisite for any "scouting and routing protocol".
Root node (center position: {0,0}) with valency: 3
Hop counts (nodes): {1,3,5,7,9,11,13,15,17,19,21}
Cumulative accessible nodes: {1,4,9,16,25,36,49,64,81,100,121}
New link counts at each hop: {0,3,12,20,28,36,44,52,60,68,76}
Cumulative accessible links: {0,3,15,35,63,99,143,195,255,323,399}
Links at hop 0: 0
Links at hop 1: 3
Sample edge node pairs: {{1,2},{1,12},{1,13},{2,3},{2,12}}
Trying to get reliable data consistency by syncing up physical clocks is just a delusion. And one that's been responsible, frankly, for decades of corrupted data. If the humble computer time stamp, that little number, is actually an unsafe way to order things, then our mission is to unpack why that is--and what architectures could possibly replace this broken model of time. It's practically a rite of passage. So what is the claim regarding clocks and consistency? Well, the first one (Newtonian time & the Minkowski fallacy) is kind of embarrassing for modern engineering--the Newtonian time error. It's this implicit assumption that all time every-where is just ticking along perfectly in sync, like there's some big universal clock in the sky. But if you're feeling left out the more sophisticated error is "necessarily" the Minkowski fallacy. Systems pay lip service to relativity, but then slide right back into the assumption that underneath it all, time exists as some smooth one-dimensional mathematical line that events just happen on. But you can't take two for two--the idea of a perfectly smooth, continuous time line requires infinite precision to define any single point on it. Computers are finite machines. You simply cannot represent infinite precision.
rows = 11;
cols = 8;
r = 1;
gap = 0.2;
dx = 2 r (Cos[\[Pi]/8] + gap);
dy = 2 r (Cos[\[Pi]/8] + gap);
markerSize = 4;
Clear[OctagonAt];
OctagonAt[{x_, y_}, rr_] :=
Polygon[Table[{x, y} +
rr RotationTransform[\[Pi]/8 + (i \[Pi])/4][{1, 0}], {i, 0, 7}]];
positions = Association[];
id = 1;
Do[positions[id] = {i dx, j dy};
id++, {j, 0, rows - 1}, {i, 0, cols - 1}];
adjacencyList = Association[];
Do[id = j cols + i + 1; adjacencyList[id] = {};
neighbors = {{i - 1, j}, {i + 1, j}, {i, j - 1}, {i, j + 1}, {i - 1,
j - 1}, {i + 1, j - 1}, {i - 1, j + 1}, {i + 1, j + 1}};
Do[Module[{ni = neighbor[[1]], nj = neighbor[[2]], nid},
If[0 <= ni < cols && 0 <= nj < rows, nid = nj cols + ni + 1;
AppendTo[adjacencyList[id], nid];];], {neighbor,
neighbors}], {j, 0, rows - 1}, {i, 0, cols - 1}];
centerI = 0;
centerJ = 0;
rootNode = centerJ cols + centerI + 1;
Print["Root node (center position ", {centerI, centerJ},
") with valency: ", Length[adjacencyList[rootNode]]];
invalidEdges = RandomInteger[50, 60];
Clear[BFS];
BFS[root_, adjList_Association] :=
Module[{distances, queue, current, neighbors},
distances = Association[root -> 0]; queue = {root};
While[queue =!= {}, current = First[queue]; queue = Rest[queue];
neighbors = adjList[current];
Do[If[! KeyExistsQ[distances, neighbor],
distances[neighbor] = distances[current] + 1;
AppendTo[queue, neighbor];], {neighbor, neighbors}];];
distances];
distances = BFS[rootNode, adjacencyList];
Clear[GetAccessibleLinksUpToHop];
GetAccessibleLinksUpToHop[maxHop_Integer] :=
Module[{accessibleLinks = {}, linkPair, uDist, vDist},
Do[Do[linkPair = Sort[{node, neighbor}];
If[! MemberQ[accessibleLinks, linkPair], uDist = distances[node];
vDist = distances[neighbor];
If[uDist <= maxHop && vDist <= maxHop &&
Min[uDist, vDist] <= maxHop - 1,
AppendTo[accessibleLinks, linkPair];];], {neighbor,
adjacencyList[node]}], {node, Keys[adjacencyList]}];
accessibleLinks];
maxHops = Max[Values[distances]] + 1;
hopCounts = Table[Count[Values[distances], h], {h, 0, maxHops}];
cumulativeNodeCounts =
Table[Count[Values[distances], x_ /; x <= h], {h, 0, maxHops}];
linkCountsAtHop =
Table[Module[{currentLinks, previousLinks},
currentLinks = GetAccessibleLinksUpToHop[h];
previousLinks = If[h > 0, GetAccessibleLinksUpToHop[h - 1], {}];
Length[currentLinks] - Length[previousLinks]], {h, 0, maxHops}];
cumulativeLinkCounts =
Table[Length[GetAccessibleLinksUpToHop[h]], {h, 0, maxHops}];
Print["Hop counts (nodes): ", hopCounts];
Print["Cumulative accessible nodes: ", cumulativeNodeCounts];
Print["New link counts at each hop: ", linkCountsAtHop];
Print["Cumulative accessible links: ", cumulativeLinkCounts];
Print["Links at hop 0: ", Length[GetAccessibleLinksUpToHop[0]]];
Print["Links at hop 1: ", Length[GetAccessibleLinksUpToHop[1]]];
edges = {};
edgeToNodePair = {};
Do[Do[Module[{edgeLine, nodePair},
edgeLine = Line[{positions[id], positions[neighbor]}];
nodePair = Sort[{id, neighbor}]; AppendTo[edges, edgeLine];
AppendTo[edgeToNodePair, nodePair];], {neighbor,
adjacencyList[id]}], {id, Keys[adjacencyList]}];
uniqueEdges = {};
uniqueNodePairs = {};
Do[If[! MemberQ[uniqueNodePairs, edgeToNodePair[[i]]],
AppendTo[uniqueEdges, edgeToNodePair[[i]]];
AppendTo[uniqueNodePairs, edgeToNodePair[[i]]];], {i,
Length[edgeToNodePair]}];
edgeToNodePair = uniqueEdges;
edges = Table[
Line[{positions[pair[[1]]], positions[pair[[2]]]}], {pair,
edgeToNodePair}];
Print["Sample edge node pairs: ", Take[edgeToNodePair, UpTo[5]]];
Clear[hopColor];
hopColor[h_] :=
ColorData["Rainbow"][Rescale[h, {0, maxHops}, {0.1, 0.9}]];
softBackground = Lighter[Gray, 0.97];
shadowOffset = {0.08, -0.08};
xRange = {Min[Values[positions][[All, 1]]] - 1.5,
Max[Values[positions][[All, 1]]] + 1.5};
yRange = {Min[Values[positions][[All, 2]]] - 1.5,
Max[Values[positions][[All, 2]]] + 1.5};
Clear[CreateGridFrame];
CreateGridFrame[currentHop_Integer] :=
Module[{accessibleNodes, accessibleLinkPairs, linkGraphics,
blackLinkCount, nodeGraphics, statusRow},
accessibleNodes =
Select[Keys[distances], distances[#1] <= currentHop &];
accessibleLinkPairs = GetAccessibleLinksUpToHop[currentHop];
linkGraphics =
Table[If[
MemberQ[accessibleLinkPairs,
edgeToNodePair[[i]]], {Directive[Thickness[0.006],
ColorData["Rainbow"][Rescale[currentHop, {0, maxHops}]],
Opacity[0.9]],
edges[[i]]}, {Directive[Thickness[0.002], GrayLevel[0.7],
Opacity[0.25]], edges[[i]]}], {i, Length[edges]}];
blackLinkCount = Length[accessibleLinkPairs];
nodeGraphics =
Table[Module[{nodeHop = distances[node], color, pos},
pos = positions[node];
color = If[nodeHop <= currentHop, hopColor[nodeHop],
Lighter[Gray, 0.8]]; {{EdgeForm[],
FaceForm[Directive[GrayLevel[0], Opacity[0.15]]],
OctagonAt[pos + shadowOffset, r 1.02]}, {EdgeForm[
Directive[GrayLevel[0.25], Thickness[0.002]]],
FaceForm[Directive[color, Specularity[White, 8]]],
OctagonAt[pos, r]}}], {node, Keys[positions]}];
statusRow =
Row[{Style["Hop ", 14, Bold, GrayLevel[0.3]],
Style[currentHop, 16, Bold, hopColor[currentHop]], Spacer[20],
Style["Nodes ", 14, Bold, GrayLevel[0.3]],
Style[Length[accessibleNodes], 16, Bold, Darker[Green, 0.2]],
Spacer[20], Style["Links ", 14, Bold, GrayLevel[0.3]],
Style[cumulativeLinkCounts[[currentHop + 1]], 16, Bold,
Darker[Blue, 0.2]], Spacer[20],
Style["New at hop ", 12, GrayLevel[0.3]],
Style[linkCountsAtHop[[currentHop + 1]], 12, Bold,
Darker[Red, 0.2]]}];
Column[{Style["Octagon Grid \[Dash] BFS Wavefront Expansion", 18,
Bold, GrayLevel[0.25]], statusRow,
Graphics[{linkGraphics, nodeGraphics}, ImageSize -> 450,
Background -> softBackground, PlotRange -> {xRange, yRange},
PlotRangePadding -> Scaled[0.05], ImagePadding -> 20,
BaseStyle -> {FontFamily -> "Helvetica", 12}]},
Spacings -> {0.8, 0.8}]];
Clear[CreateNodeGraphFrame];
CreateNodeGraphFrame[currentHop_Integer] :=
Module[{currentHopCounts, currentCumulative, hopRange},
currentHopCounts = hopCounts[[1 ;; currentHop + 1]];
currentCumulative = cumulativeNodeCounts[[1 ;; currentHop + 1]];
hopRange = Range[0, currentHop];
ListLinePlot[{Transpose[{hopRange, currentHopCounts}],
Transpose[{hopRange, currentCumulative}]},
PlotStyle -> {Directive[ColorData["Rainbow"][0.15],
Thickness[0.006]],
Directive[ColorData["Rainbow"][0.75], Thickness[0.006], Dashed]},
PlotMarkers -> {{Automatic, markerSize}, {Automatic, markerSize}},
Filling -> {2 -> {1}}, Background -> softBackground,
Frame -> True, Axes -> False,
FrameLabel -> {Style["Hop count", 12, GrayLevel[0.2]],
Style["Number of nodes", 12, GrayLevel[0.2]]},
PlotLabel -> Style["Node Accessibility vs Hop Count", 14, Bold],
GridLines -> {Range[0, maxHops, 2], Automatic},
GridLinesStyle -> Directive[GrayLevel[0.85], Dashed],
ImageSize -> 420,
PlotRange -> {{0, maxHops}, {0, 1.05 Max[cumulativeNodeCounts]}},
PlotLegends -> {"Nodes at each hop", "Cumulative accessible nodes"},
BaseStyle -> {FontFamily -> "Helvetica", 11}]];
Clear[CreateLinkGraphFrame];
CreateLinkGraphFrame[currentHop_Integer] :=
Module[{currentLinkCounts, currentCumulativeLinks, hopRange,
theoreticalMax},
currentLinkCounts = linkCountsAtHop[[1 ;; currentHop + 1]];
currentCumulativeLinks = cumulativeLinkCounts[[1 ;; currentHop + 1]];
hopRange = Range[0, currentHop];
theoreticalMax = 4 (rows - 1) (cols - 1) + rows + cols - 2;
ListLinePlot[{Transpose[{hopRange, currentLinkCounts}],
Transpose[{hopRange, currentCumulativeLinks}]},
PlotStyle -> {Directive[ColorData["Rainbow"][0.35],
Thickness[0.006]],
Directive[ColorData["Rainbow"][0.9], Thickness[0.006], Dashed]},
PlotMarkers -> {{Automatic, markerSize}, {Automatic, markerSize}},
Background -> softBackground, Frame -> True, Axes -> False,
FrameLabel -> {Style["Hop count", 12, GrayLevel[0.2]],
Style["Number of links", 12, GrayLevel[0.2]]},
PlotLabel -> Style["Link Accessibility vs Hop Count", 14, Bold],
GridLines -> {Range[0, maxHops, 2], Automatic},
GridLinesStyle -> Directive[GrayLevel[0.85], Dashed],
ImageSize -> 900,
PlotRange -> {{0, maxHops}, {0, 1.05 theoreticalMax}},
PlotLegends -> {"New links at each hop",
"Cumulative accessible links"},
BaseStyle -> {FontFamily -> "Helvetica", 11}]];
animation =
Animate[Column[{Row[{CreateGridFrame[h], Spacer[25],
CreateNodeGraphFrame[h]}], Spacer[15], CreateLinkGraphFrame[h]},
Spacings -> {1.0, 1.0}], {h, 0, maxHops, 1}, AnimationRate -> 1,
AnimationDirection -> Forward, AnimationRepetitions -> \[Infinity]];
animation
Root node (center position {0,0}) with valency: 3
Hop counts (nodes): {1,3,5,7,9,11,13,15,8,8,8,0}
Cumulative accessible nodes: {1,4,9,16,25,36,49,64,72,80,88,88}
New link counts at each hop: {0,3,12,20,28,36,44,52,37,29,29,7}
Cumulative accessible links: {0,3,15,35,63,99,143,195,232,261,290,297}
Links at hop 0: 0
Links at hop 1: 3
Sample edge node pairs: {{1,2},{1,9},{1,10},{2,3},{2,10}}
Those last few decimal places in the timestamp are essentially meaningless noise. The order is arbitrary--but the database saves and treats it as gospel truth. That leads directly to an incorrect causal ordering of events. What really happened first might be different, but the log has already decided--and it's wrong.
TCP is a classic example of the Minkowski error in action. It tries to build a shared timeline between two endpoints, and when that shared understanding fails, you get unrecoverable data corruption--or your browser just gives up after a few tries. It's not so much a reversal as it is a continuation of the protocol which tries to force a direction in time using monotonic sequence numbers. But when the network state is lost, those numbers become totally ambiguous. The protocol has no reliable way left to figure out which data exchange truly came before another across that gap.
Analyzing Accessibility vs. Hop Count
A survivable metric for any network will always be the relationship between hop count, node accessibility, and link accessibility. This defines the network's diameter and cost of communication. We calculate the nodes and new links discovered at each hop.
ClearAll["Global`*"];
rows = 11;
cols = 11;
r = 1;
gap = 0.20;
dx = 2 r (Cos[\[Pi]/8] + gap);
dy = 2 r (Cos[\[Pi]/8] + gap);
OctagonAt[{x_, y_}, rad_] :=
Polygon[Table[{x, y} +
rad RotationTransform[\[Pi]/8 + (i \[Pi])/4][{1, 0}], {i, 0, 7}]];
positions =
Association[
Flatten[Table[
With[{id = j cols + i + 1}, id -> {i dx, j dy}], {j, 0,
rows - 1}, {i, 0, cols - 1}], 1]];
adjacencyList =
Association[
Flatten[Table[
With[{id = j cols + i + 1},
Module[{nbrIdx, validNbrs},
nbrIdx = {{i - 1, j}, {i + 1, j}, {i, j - 1}, {i,
j + 1}, {i - 1, j - 1}, {i + 1, j - 1}, {i - 1,
j + 1}, {i + 1, j + 1}};
validNbrs =
Select[nbrIdx, 0 <= #1[[1]] < cols && 0 <= #1[[2]] < rows &];
id -> (validNbrs /. {ii_, jj_} :> jj cols + ii + 1)]], {j, 0,
rows - 1}, {i, 0, cols - 1}], 1]];
centerI = Floor[cols/2];
centerJ = Floor[rows/2];
rootNode = centerJ cols + centerI + 1;
Print[Style[
Row[{"Root node: (center position: ", {centerI, centerJ},
") with valency: ", Length[adjacencyList[rootNode]]}], 14, Bold]];
BFS[root_, adj_Association] :=
Module[{distances, queue, current, neighbors},
distances = Association[root -> 0]; queue = {root};
While[queue =!= {}, current = First[queue]; queue = Rest[queue];
neighbors = adj[current];
Do[If[! KeyExistsQ[distances, nbr],
distances[nbr] = distances[current] + 1;
queue = Append[queue, nbr];], {nbr, neighbors}];]; distances];
distances = BFS[rootNode, adjacencyList];
maxHops = Max[Values[distances]];
edgeAssoc = Association[];
Do[Do[With[{pair = Sort[{id, nbr}]},
If[! KeyExistsQ[edgeAssoc, pair],
edgeAssoc[pair] =
Line[{positions[id], positions[nbr]}];];], {nbr,
adjacencyList[id]}], {id, Keys[adjacencyList]}];
edgeToNodePair = Keys[edgeAssoc];
edges = Values[edgeAssoc];
Print["Sample edge node pairs: ", Take[edgeToNodePair, UpTo[5]]];
firstHopList =
Table[Module[{u, v, du, dv, m, M}, u = pair[[1]]; v = pair[[2]];
du = distances[u]; dv = distances[v]; m = Min[du, dv];
M = Max[du, dv]; Max[M, m + 1]], {pair, edgeToNodePair}];
firstHopList = (Min[#1, maxHops] &) /@ firstHopList;
edgeFirstHopAssoc = AssociationThread[edgeToNodePair -> firstHopList];
accessibleEdgePairsPerHop =
Table[Pick[edgeToNodePair, UnitStep[h - firstHopList], 1], {h, 0,
maxHops}];
GetAccessibleLinksUpToHop[h_Integer] :=
accessibleEdgePairsPerHop[[h + 1]];
hopCounts = Table[Count[Values[distances], h], {h, 0, maxHops}];
cumulativeNodeCounts =
Table[Count[Values[distances], x_ /; x <= h], {h, 0, maxHops}];
linkCountsAtHop = Table[Count[firstHopList, h], {h, 0, maxHops}];
cumulativeLinkCounts =
Table[Count[firstHopList, _?(#1 <= h &)], {h, 0, maxHops}];
Print["Hop counts (nodes): ", hopCounts];
Print["Cumulative accessible nodes: ", cumulativeNodeCounts];
Print["New link counts at each hop: ", linkCountsAtHop];
Print["Cumulative accessible links: ", cumulativeLinkCounts];
Print["Links at hop 0: ", Length[GetAccessibleLinksUpToHop[0]]];
Print["Links at hop 1: ", Length[GetAccessibleLinksUpToHop[1]]];
hopPalette[hop_, maxHop_] :=
ColorData["DarkRainbow"][Rescale[hop, {0, maxHop}]];
posArray = Values[positions];
{xMin, xMax} = MinMax[posArray[[All, 1]]];
{yMin, yMax} = MinMax[posArray[[All, 2]]];
plotRange2D = {{xMin - 1.5, xMax + 1.5}, {yMin - 1.5, yMax + 1.5}};
maxRange = 4 (rows - 1) (cols - 1) + rows + cols - 2;
CreateGridFrame[currentHop_Integer] :=
Module[{accessibleNodes, accessibleLinkPairs, linkGraphics,
nodeGraphics, blackLinkCount},
accessibleNodes =
Select[Keys[distances], distances[#1] <= currentHop &];
accessibleLinkPairs = GetAccessibleLinksUpToHop[currentHop];
linkGraphics =
Table[Module[{pair = edgeToNodePair[[i]], base = edges[[i]],
styleActive, styleInactive},
styleActive =
Directive[ColorData["BrightBands"][0.15], Opacity[0.9],
Thickness[0.006]];
styleInactive =
Directive[GrayLevel[0.6], Opacity[0.25], Thickness[0.002]];
If[MemberQ[accessibleLinkPairs, pair], {styleActive,
base}, {styleInactive, base}]], {i, Length[edges]}];
blackLinkCount = Length[accessibleLinkPairs];
nodeGraphics =
Table[Module[{nodeHop, col, baseStyle, inactiveStyle},
nodeHop = distances[node]; col = hopPalette[nodeHop, maxHops];
baseStyle = {EdgeForm[{GrayLevel[0.1], Thickness[0.003]}],
Glow[Directive[col, Opacity[0.85]]],
FaceForm[Directive[col, Opacity[0.95]]]};
inactiveStyle = {EdgeForm[{GrayLevel[0.4], Thickness[0.0015]}],
FaceForm[Directive[GrayLevel[0.8], Opacity[0.4]]]};
If[nodeHop <= currentHop, {baseStyle,
OctagonAt[positions[node], r]}, {inactiveStyle,
OctagonAt[positions[node], r]}]], {node, Keys[positions]}];
Column[{Style[
Row[{"Hop: ", currentHop, " | Accessible Nodes: ",
Length[accessibleNodes], " | Accessible Links: ",
cumulativeLinkCounts[[currentHop + 1]],
" | Active Links This Frame: ", blackLinkCount}], 13,
Black, Bold],
Graphics[{{Directive[GrayLevel[0.97], Opacity[1]],
Rectangle[{xMin - 2, yMin - 2}, {xMax + 2, yMax + 2}]},
linkGraphics,
nodeGraphics, {Directive[Black, Thickness[0.006], Opacity[0.9]],
Circle[positions[rootNode], 1.15 r]}}, Background -> White,
PlotRange -> plotRange2D, ImageSize -> 420, Frame -> True,
FrameStyle -> Directive[GrayLevel[0.3], Thickness[0.002]],
PlotRangePadding -> Scaled[0.05]]}]];
CreateNodeGraphFrame[currentHop_Integer] :=
Module[{currentHopCounts, currentCumulativeNodes,
currentCumulativeLinks, dataLinks, dataNodes},
currentHopCounts = hopCounts[[1 ;; currentHop + 1]];
currentCumulativeNodes = cumulativeNodeCounts[[1 ;; currentHop + 1]];
currentCumulativeLinks =
cumulativeLinkCounts[[1 ;; currentHop + 1]];
dataLinks =
Transpose[{Range[0, currentHop], currentCumulativeLinks}];
dataNodes =
Transpose[{Range[0, currentHop], currentCumulativeNodes}];
ListLinePlot[{dataLinks, dataNodes},
PlotStyle -> {Directive[ColorData["BrightBands"][0.20], Thick],
Directive[ColorData["BrightBands"][0.7], Thick, Dashed]},
PlotMarkers -> {{Automatic, 4}, {Automatic, 4}}, Frame -> True,
FrameLabel -> {Style["Hop Count", 13, GrayLevel[0.20]],
Style["Cumulative Count", 13, GrayLevel[0.20]]},
PlotLabel ->
Style["Accessibility vs. Hop Distance", 14, Bold, Black],
GridLines -> {Range[0, maxHops, 2], None},
GridLinesStyle ->
Directive[GrayLevel[0.85], Dashed, Thickness[0.0015]],
Background -> White,
FrameStyle -> Directive[GrayLevel[0.3], Thickness[0.002]],
TicksStyle -> Directive[GrayLevel[0.25], 10],
PlotRange -> {{0, maxHops}, {0, maxRange}}, ImageSize -> 420,
PlotRangePadding -> Scaled[0.05],
PlotLegends ->
Placed[{"Cumulative accessible links",
"Cumulative accessible nodes"}, {0.55, 0.9}]]];
frames =
Table[Row[{CreateGridFrame[h], Spacer[20], CreateNodeGraphFrame[h]},
ImageSize -> 900], {h, 0, maxHops}];
animation =
Animate[Row[{CreateGridFrame[h], Spacer[20], CreateNodeGraphFrame[h]},
ImageSize -> 900], {h, 0, maxHops, 1}, AnimationRate -> 1,
AnimationDirection -> Forward, DefaultDuration -> maxHops + 1];
ListAnimate[frames];
Export["hopLinks_sidebyside_beautiful.gif", frames,
"DisplayDurations" -> 1];
animation
At the end of the day, you cannot engineer your way around the fundamental laws of physics. It is absolutely impossible to synchronize clocks perfectly. Clocks can't be synchronized in time; they can only be synchronized in frequency. That distinction is absolutely everything.
I suppose a rough analogy would be if you took the derivation of the Lorentz constant or, who knew the Lorentz constant like we do. Time seems to be tied directly to information exchange. When an agent receives information, time goes forward locally for that agent. But when it emits or loses information, its frame of reference shifts in a complex way.

Root node: (center position: {5,5}) with valency: 8
Sample edge node pairs: {{1,2},{1,12},{1,13},{2,3},{2,13}}
Hop counts (nodes): {1,8,16,24,32,40}
Cumulative accessible nodes: {1,9,25,49,81,121}
New link counts at each hop: {0,8,44,76,108,184}
Cumulative accessible links: {0,8,52,128,236,420}
Links at hop 0: 0
Links at hop 1: 8
Physicalizing the Scouting Wavefront
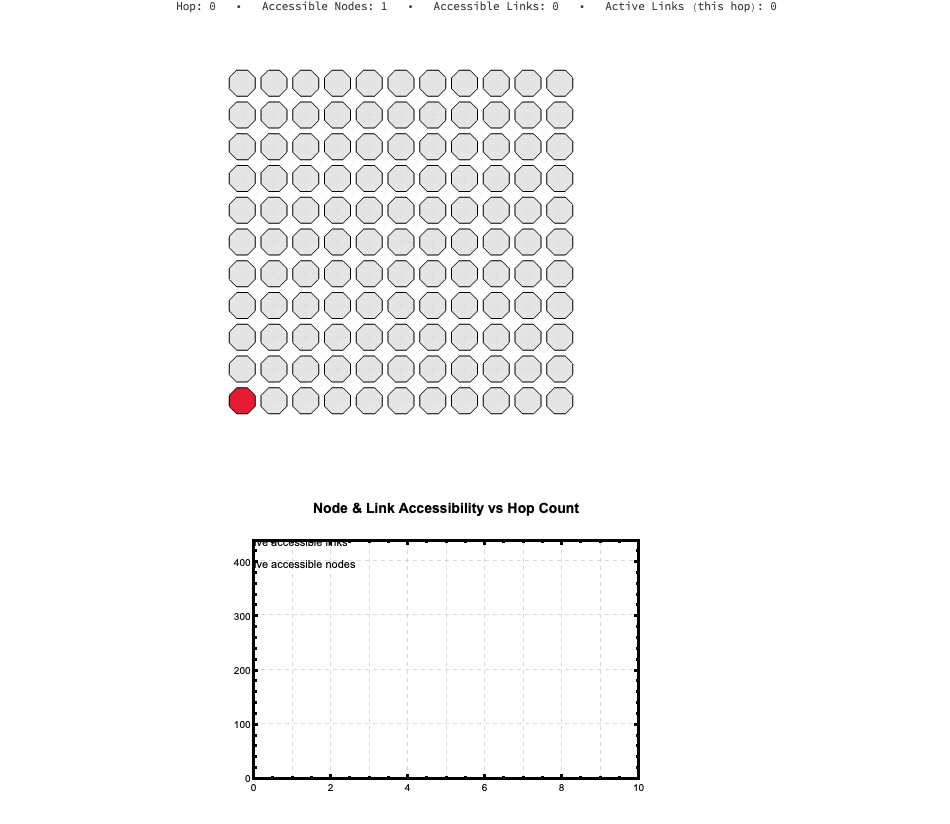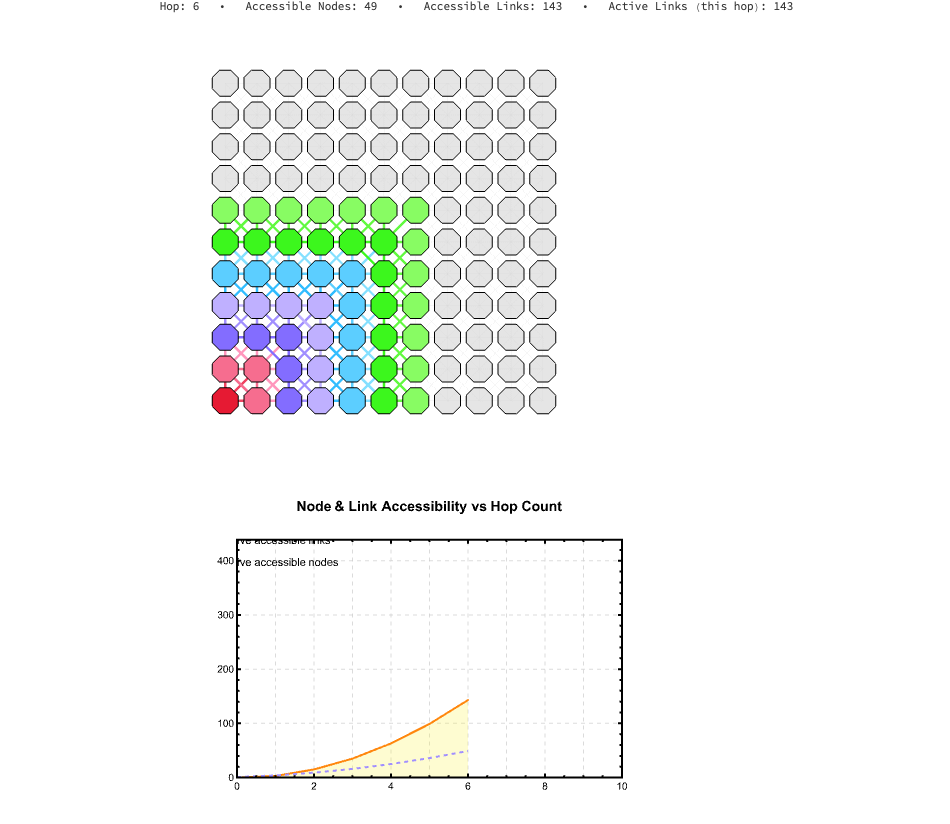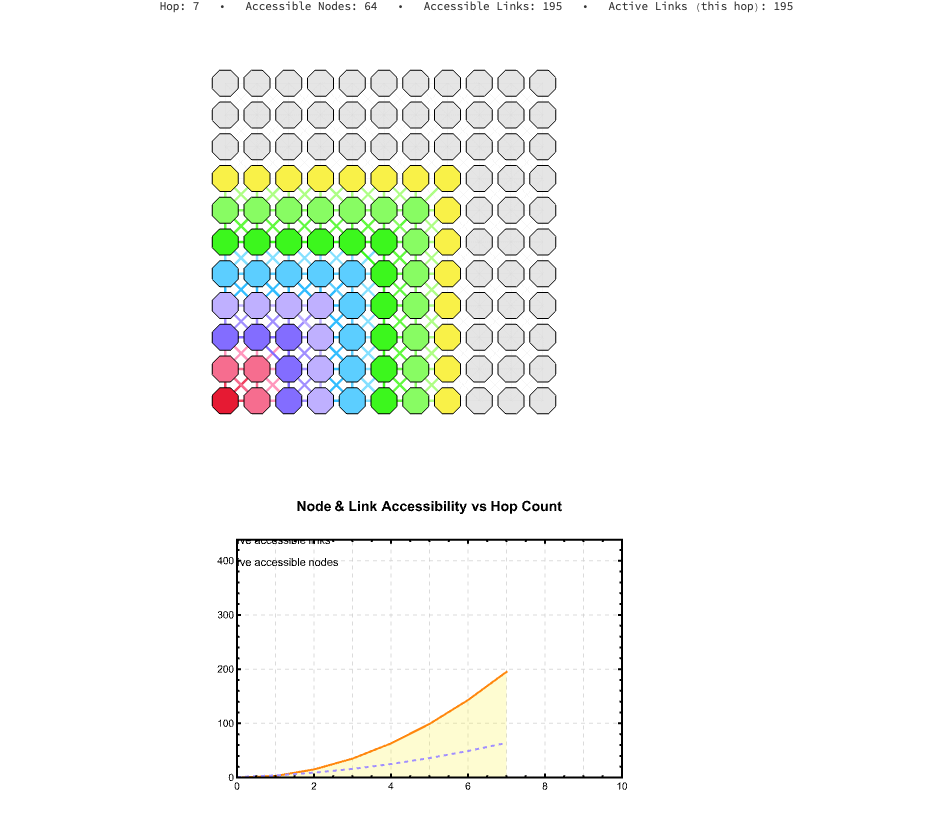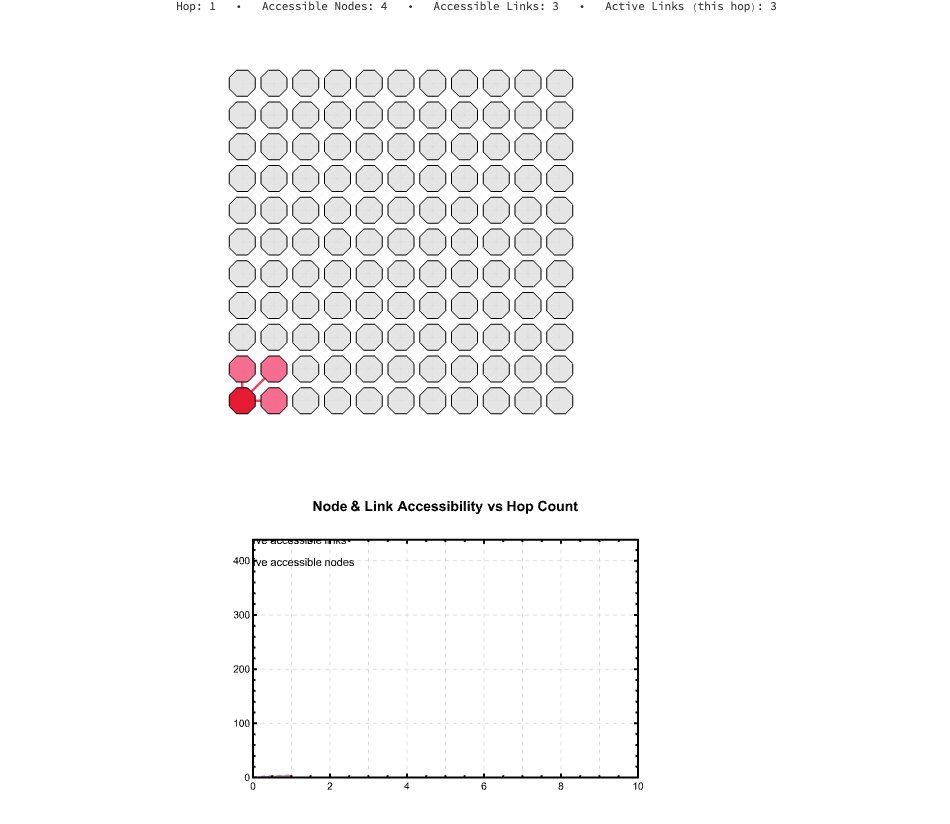
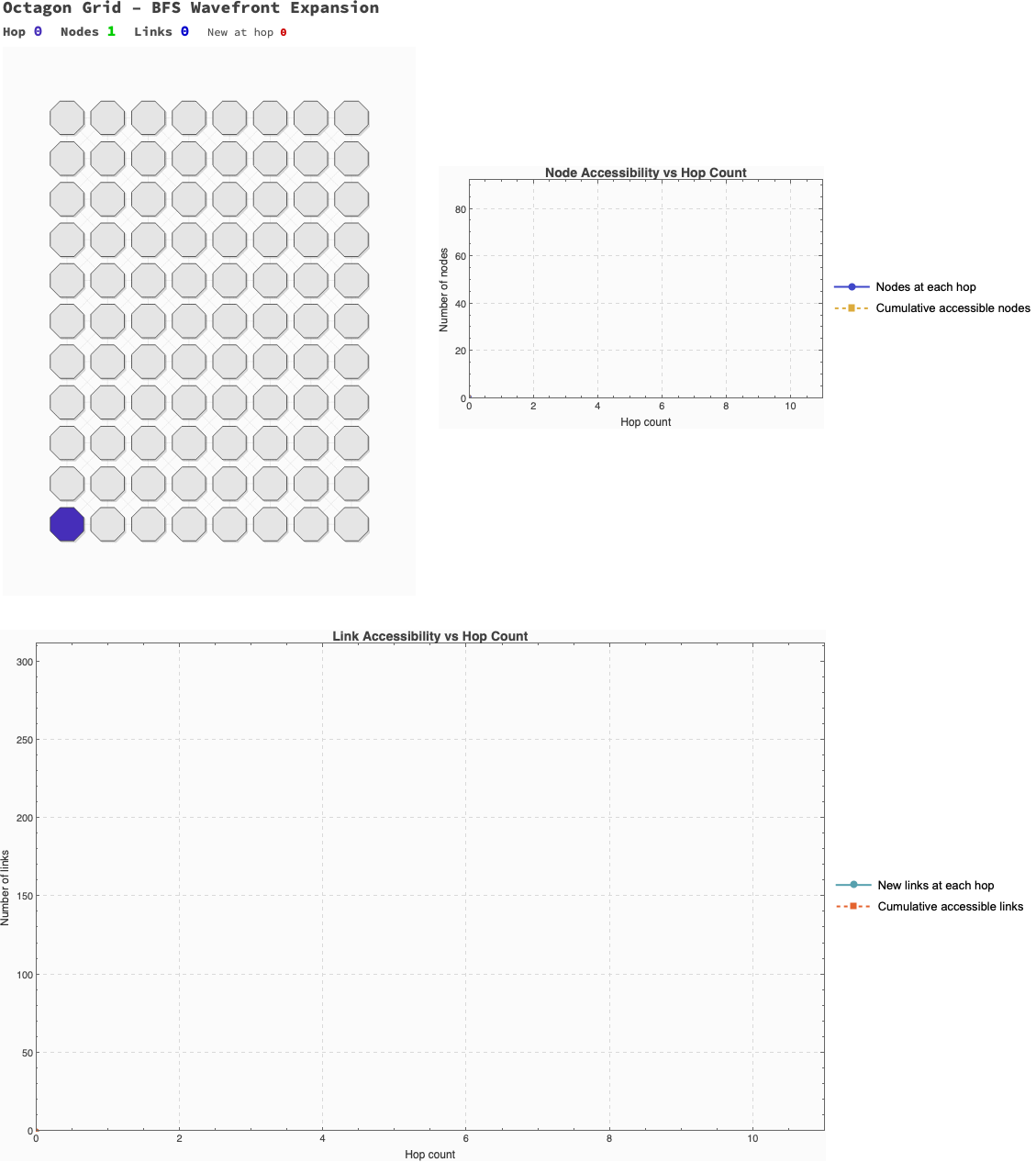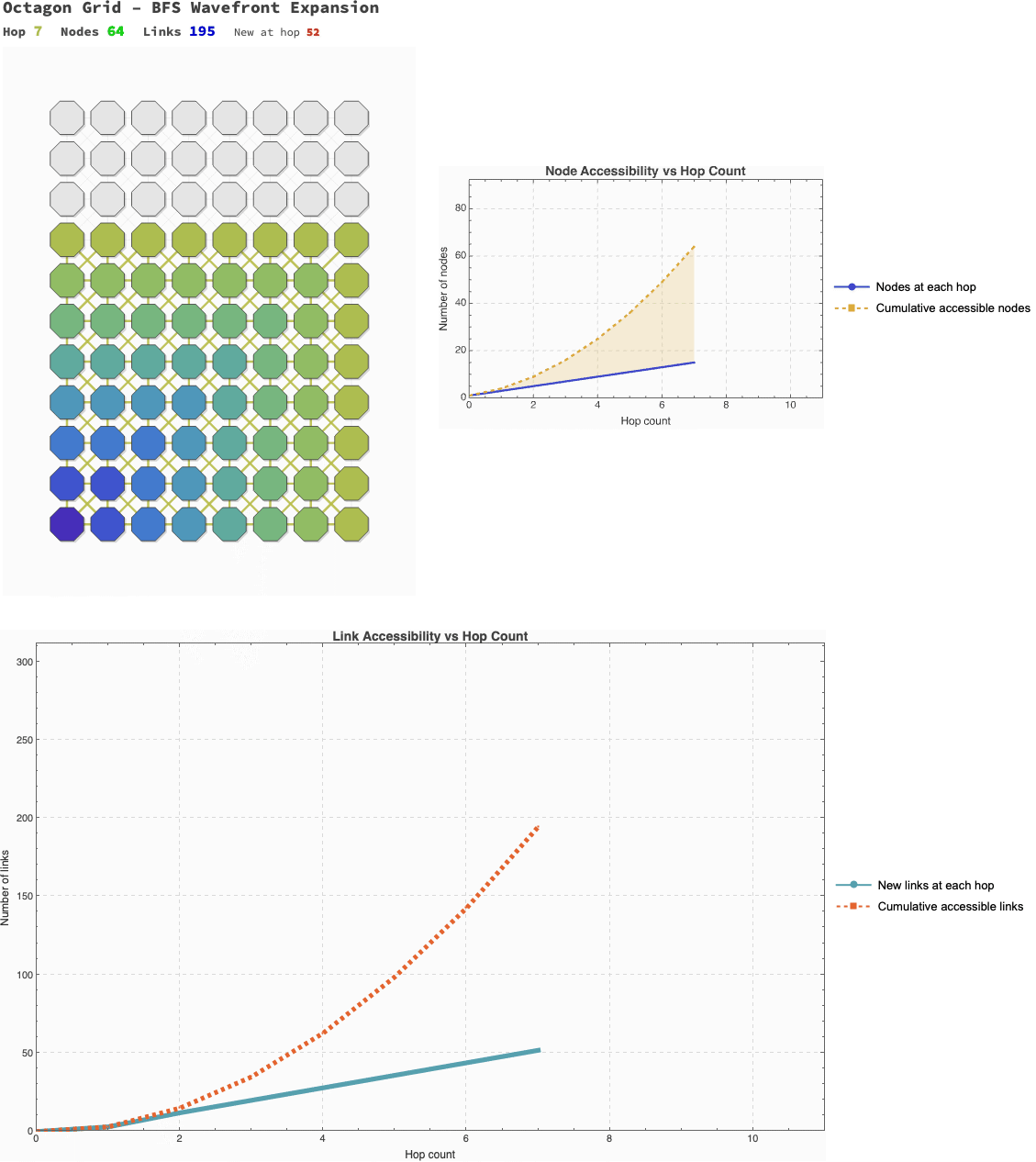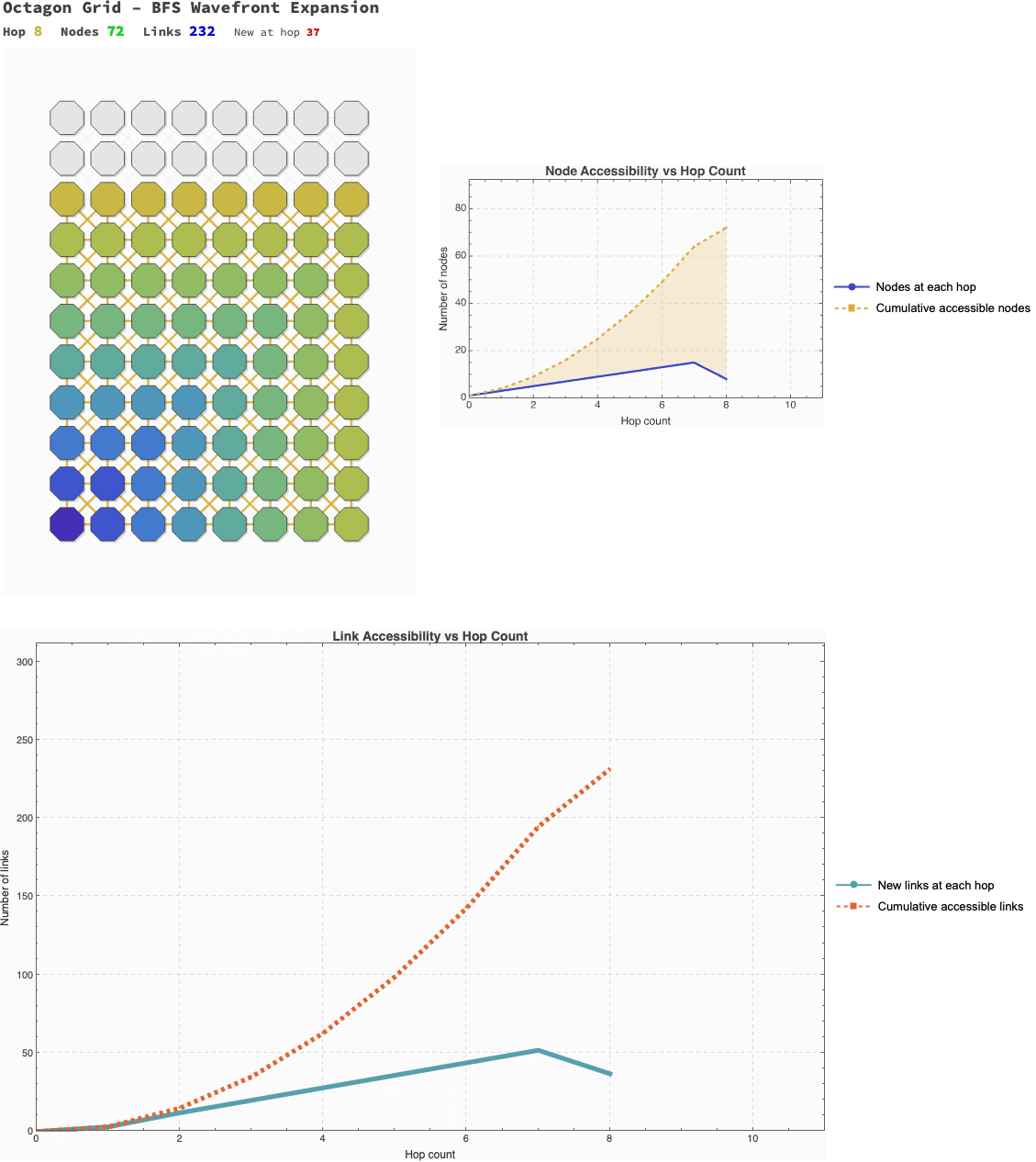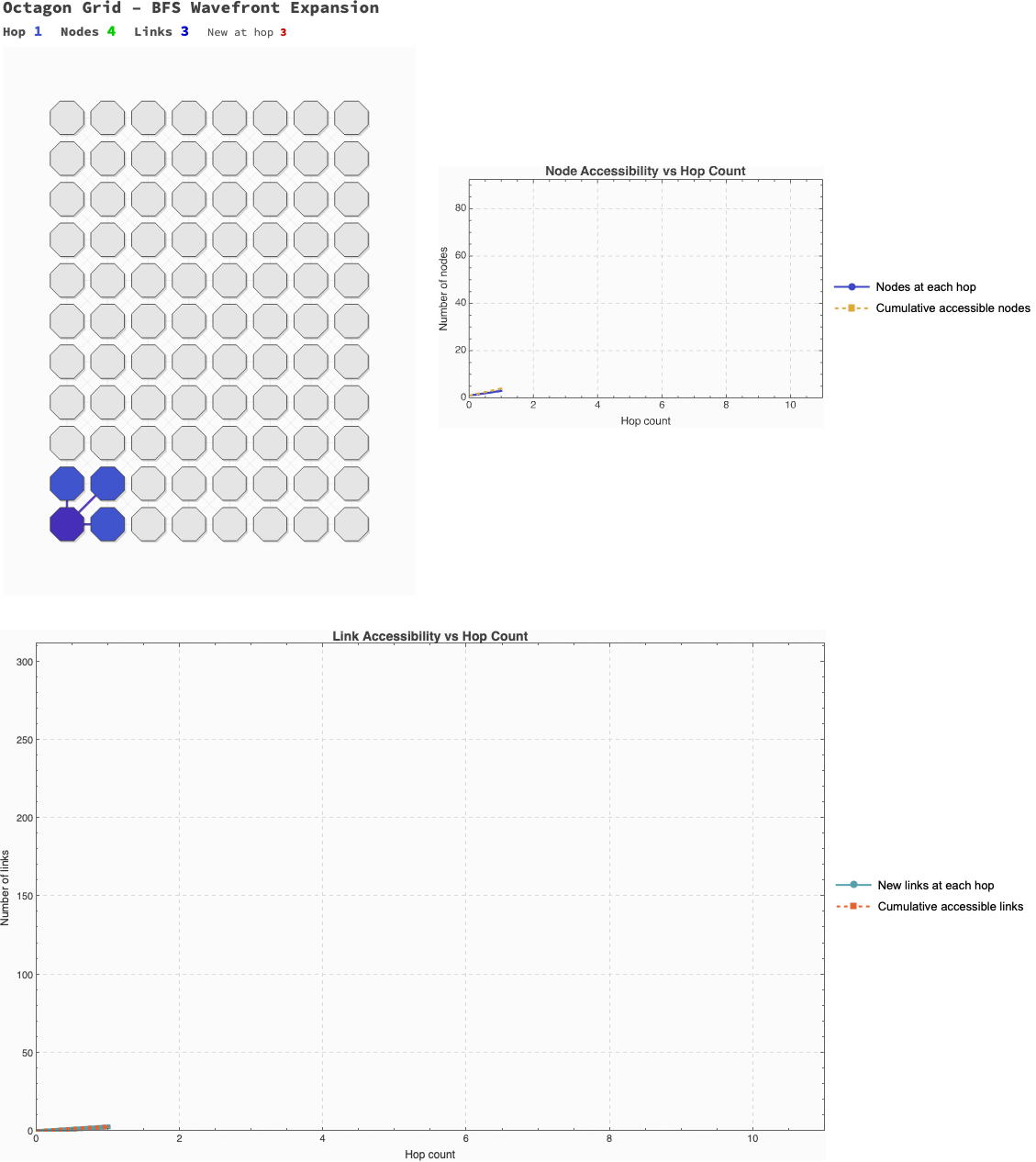
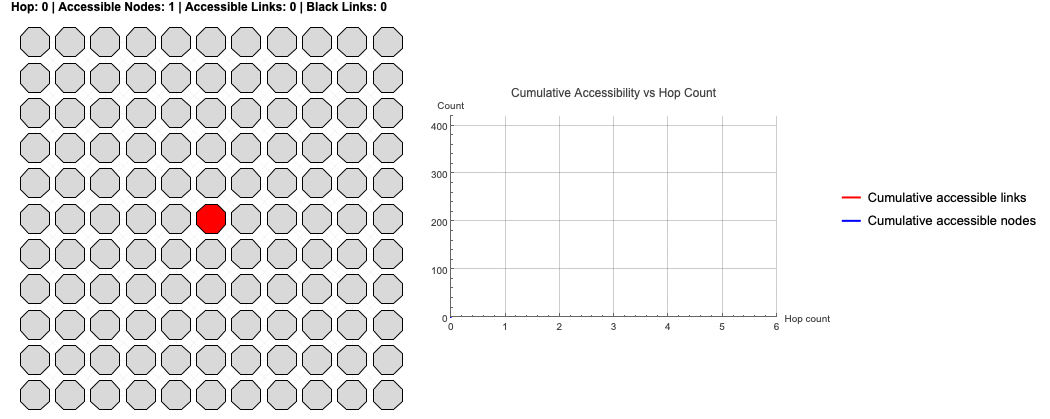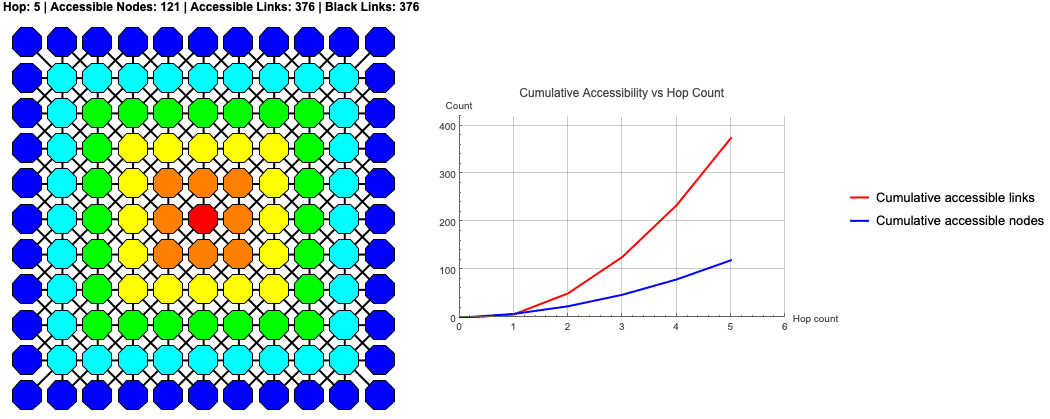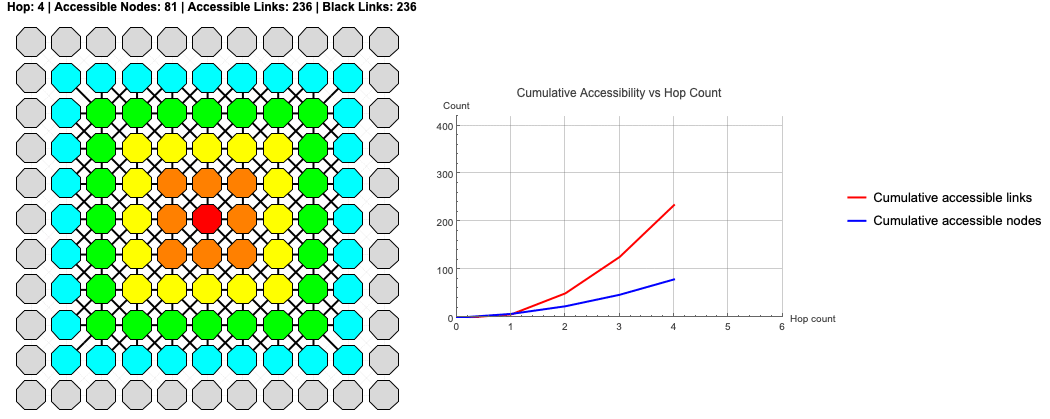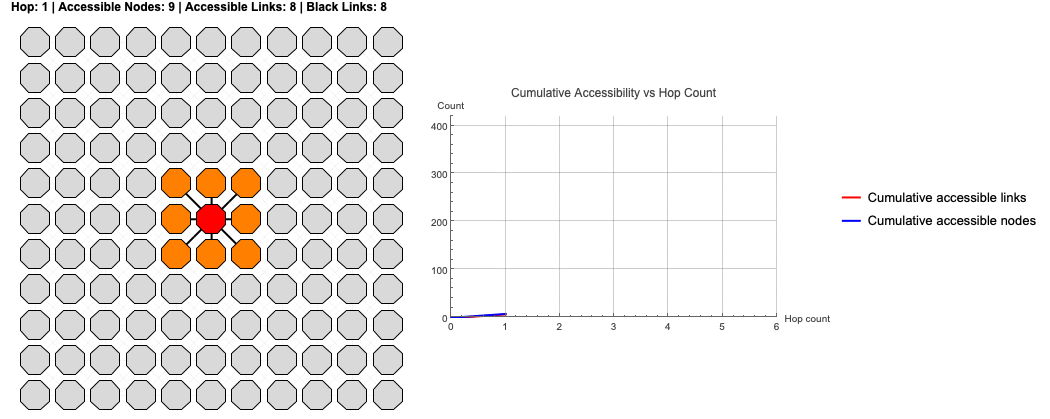
Now we combine these elements into a visualization. The following code generates an animation of the BFS wavefront expanding. The left panel shows the "scouting" process on the lattice itself, coloring nodes by their hop distance. The right panel plots the cumulative growth of accessible nodes and links.
This isn't just a "pretty picture"; it's a model of discovery. We are watching the rootNode build its map of the reachable world.
ClearAll[rows, cols, r, gap, dx, dy, OctagonAt, positions,
originalAdjacencyList, RemoveEdges, AnimatedBFS, allEdges, rootNode,
centerI, centerJ];
rows = 11;
cols = 11;
r = 1;
gap = 0.2;
dx = 2 r (Cos[\[Pi]/8] + gap);
dy = 2 r (Cos[\[Pi]/8] + gap);
OctagonAt[{x_, y_}, rr_] :=
GeometricTransformation[RegularPolygon[{x, y}, rr, 8],
RotationTransform[\[Pi]/8, {x, y}]];
positions = Association[];
Module[{id = 1},
Do[positions[id] = {i dx, j dy};
id++, {j, 0, rows - 1}, {i, 0, cols - 1}];];
originalAdjacencyList = Association[];
Do[Module[{id = j cols + i + 1, neighbors, validNeighbors},
neighbors = {{i - 1, j}, {i + 1, j}, {i, j - 1}, {i,
j + 1}, {i - 1, j - 1}, {i + 1, j - 1}, {i - 1, j + 1}, {i + 1,
j + 1}};
validNeighbors =
Select[neighbors, 0 <= #1[[1]] < cols && 0 <= #1[[2]] < rows &];
originalAdjacencyList[id] = (#1[[2]] cols + #1[[1]] + 1 &) /@
validNeighbors;], {j, 0, rows - 1}, {i, 0, cols - 1}];
centerI = 0;
centerJ = 0;
rootNode = centerJ cols + centerI + 1;
Print[Style["BFS Root Node Diagnostics", 14, Bold, Black], "\n",
"Root node: ", rootNode, " (grid position: ", {centerI, centerJ}, ")",
" with valency: ", Length[originalAdjacencyList[rootNode]]];
allEdges =
DeleteDuplicates[
Reap[Do[With[{id = key},
Sow /@ Sort /@
Select[Thread[{id,
originalAdjacencyList[id]}], #1[[1]] < #1[[2]] &]], {key,
Keys[originalAdjacencyList]}]][[2, 1]]];
Print["Total edges in graph: ", Length[allEdges]];
RemoveEdges[adjList_, edgesToRemove_List] :=
Module[{newAdjList = Association[adjList]},
Do[With[{u = edge[[1]], v = edge[[2]]},
newAdjList[u] = DeleteCases[newAdjList[u], v];
newAdjList[v] = DeleteCases[newAdjList[v], u];], {edge,
edgesToRemove}]; newAdjList];
AnimatedBFS[root_, adjList_Association] :=
Module[{distances, parentMap, queue, current, neighbors, steps},
distances = Association[root -> 0]; parentMap = Association[];
queue = {root}; steps = {Association[distances]};
While[queue =!= {}, current = First[queue]; queue = Rest[queue];
neighbors = Lookup[adjList, current, {}];
Do[If[! KeyExistsQ[distances, neighbor],
distances[neighbor] = distances[current] + 1;
parentMap[neighbor] = current; AppendTo[queue, neighbor];
AppendTo[steps, Association[distances]];], {neighbor,
neighbors}];]; {distances, parentMap, steps}];
DynamicModule[{numFailedEdges = 0, failedEdges = {},
currentReachable = Length[Keys[originalAdjacencyList]],
currentUnreachable = 0, finalDistances = Association[],
finalParentMap = Association[], bfsSteps = {},
currentAdjList = originalAdjacencyList,
maxFailures = Min[50, Length[allEdges]], animationRunning = False,
currentStep = 0, maxSteps = 0,
animationSpeed = 0.4}, {finalDistances, finalParentMap, bfsSteps} =
AnimatedBFS[rootNode, currentAdjList];
currentReachable = Length[Keys[finalDistances]];
currentUnreachable =
Length[Keys[originalAdjacencyList]] - currentReachable;
maxSteps = Max[0, Length[bfsSteps] - 1];
Column[{Panel[
Column[{Style["Network Failure & BFS Controls", 16, Bold, Black,
FontFamily -> "Helvetica"],
Row[{"Number of failed edges: ",
Slider[Dynamic[numFailedEdges], {0, Length[allEdges], 1}],
Spacer[8],
Panel[Dynamic[numFailedEdges], Background -> White,
FrameMargins -> {{6, 6}, {2, 2}}]}],
Row[{"Animation speed (seconds/step): ",
Slider[Dynamic[animationSpeed], {0.1, 2.0, 0.1}], Spacer[8],
Dynamic[NumberForm[animationSpeed, {2, 1}]]}],
Row[{Style["Reachable nodes: ", Bold, Darker[Green]],
Dynamic[currentReachable], Spacer[20],
Style["Unreachable nodes: ", Bold, Darker[Red]],
Dynamic[currentUnreachable]}],
Row[{Button[Style["Random Edge Failures", 12, Bold, Black],
failedEdges =
If[numFailedEdges > 0,
RandomSample[allEdges, numFailedEdges], {}];
currentAdjList =
RemoveEdges[originalAdjacencyList,
failedEdges]; {finalDistances, finalParentMap, bfsSteps} =
AnimatedBFS[rootNode, currentAdjList];
currentReachable = Length[Keys[finalDistances]];
currentUnreachable =
Length[Keys[originalAdjacencyList]] - currentReachable;
maxSteps = Max[0, Length[bfsSteps] - 1]; currentStep = 0;
animationRunning = False;], Spacer[10],
Button[Style["Start BFS Animation", 12, Bold, Black],
If[Length[bfsSteps] > 0, currentStep = 0;
animationRunning = True;]], Spacer[10],
Button[Style["Reset All Links", 12, Bold, Black],
failedEdges = {}; numFailedEdges = 0;
currentAdjList =
originalAdjacencyList; {finalDistances, finalParentMap,
bfsSteps} = AnimatedBFS[rootNode, currentAdjList];
currentReachable = Length[Keys[finalDistances]];
currentUnreachable = 0;
maxSteps = Max[0, Length[bfsSteps] - 1]; currentStep = 0;
animationRunning = False;]}],
If[maxSteps > 0,
Row[{"Animation step: ",
Slider[Dynamic[currentStep], {0, maxSteps, 1}], Spacer[6],
Dynamic[Style[Row[{currentStep, " / ", maxSteps}], 11, Bold,
Black]]}], Nothing]}, Spacings -> 1.2, BaseStyle -> {Black}],
Background -> Lighter[Blend[{Gray, Blue}, 0.15], 0.85],
FrameMargins -> Medium,
FrameStyle -> Directive[GrayLevel[0.4], Thickness[0.003]]],
Dynamic[If[animationRunning && currentStep < maxSteps,
Pause[animationSpeed]; currentStep++;
If[currentStep >= maxSteps, animationRunning = False];]; ""],
Dynamic[Module[{workingEdges, workingCoords, failedCoords,
failedEdgeLines, workingEdgeLines, nodeGraphics, arrowGraphics,
currentDistancesStep, visibleNodes, coords, minX, maxX, minY,
maxY, maxKnownDist, distanceColor, totalNodes},
totalNodes = Length[Keys[originalAdjacencyList]];
currentDistancesStep =
If[Length[bfsSteps] > 0 && 0 <= currentStep < Length[bfsSteps],
bfsSteps[[currentStep + 1]], Association[]];
visibleNodes = Keys[currentDistancesStep];
workingEdges = Complement[allEdges, failedEdges];
workingCoords = (positions /@ #1 &) /@ workingEdges;
failedCoords = (positions /@ #1 &) /@ failedEdges;
coords =
Values[positions]; {minX, maxX} = {Min[coords[[All, 1]]],
Max[coords[[All, 1]]]}; {minY, maxY} = {Min[coords[[All, 2]]],
Max[coords[[All, 2]]]};
maxKnownDist =
If[finalDistances === Association[], 1,
Max[Values[finalDistances]]];
distanceColor[d_] :=
ColorData["SolarColors"][Rescale[d, {0, maxKnownDist}, {0, 1}]];
failedEdgeLines =
If[failedCoords === {}, {}, {Glow[Red],
Directive[Red, Thickness[0.012], Dashed, CapForm["Round"]],
Line /@ failedCoords}];
workingEdgeLines =
If[workingCoords === {}, {}, {Directive[GrayLevel[0.25, 0.6],
Thickness[0.004]], CapForm["Round"], Line /@ workingCoords}];
nodeGraphics =
Table[Module[{pt = positions[node]},
Which[node === rootNode, {EdgeForm[{Black, Thick}],
FaceForm[RGBColor[0.9, 0.4, 0.3]], OctagonAt[pt, 1.1 r]},
MemberQ[visibleNodes,
node], {EdgeForm[{Darker[Green, 0.4], Thickness[0.005]}],
FaceForm[distanceColor[currentDistancesStep[node]]],
OctagonAt[pt, r]},
KeyExistsQ[finalDistances,
node], {EdgeForm[{GrayLevel[0.4], Thickness[0.003]}],
FaceForm[Directive[GrayLevel[0.9], Opacity[0.9]]],
OctagonAt[pt, r]},
True, {EdgeForm[{GrayLevel[0.7], Thickness[0.002]}],
FaceForm[Directive[RGBColor[0.9, 0.7, 0.8], Opacity[0.6]]],
OctagonAt[pt, r]}]], {node, Keys[positions]}];
arrowGraphics =
If[finalParentMap === Association[], {},
Table[If[
KeyExistsQ[finalParentMap, node] &&
MemberQ[visibleNodes, node], {Directive[
RGBColor[0.1, 0.4, 0.9], Thickness[0.008]],
Arrowheads[0.03],
Arrow[{positions[finalParentMap[node]], positions[node]}]},
Nothing], {node, Keys[finalParentMap]}]];
EventHandler[
Graphics[{{FaceForm[Lighter[Blend[{Blue, Black}, 0.9], 0.9]],
EdgeForm[None],
Rectangle[{minX - 10, minY - 10}, {maxX + 10, maxY + 10}]},
workingEdgeLines, failedEdgeLines, nodeGraphics,
arrowGraphics,
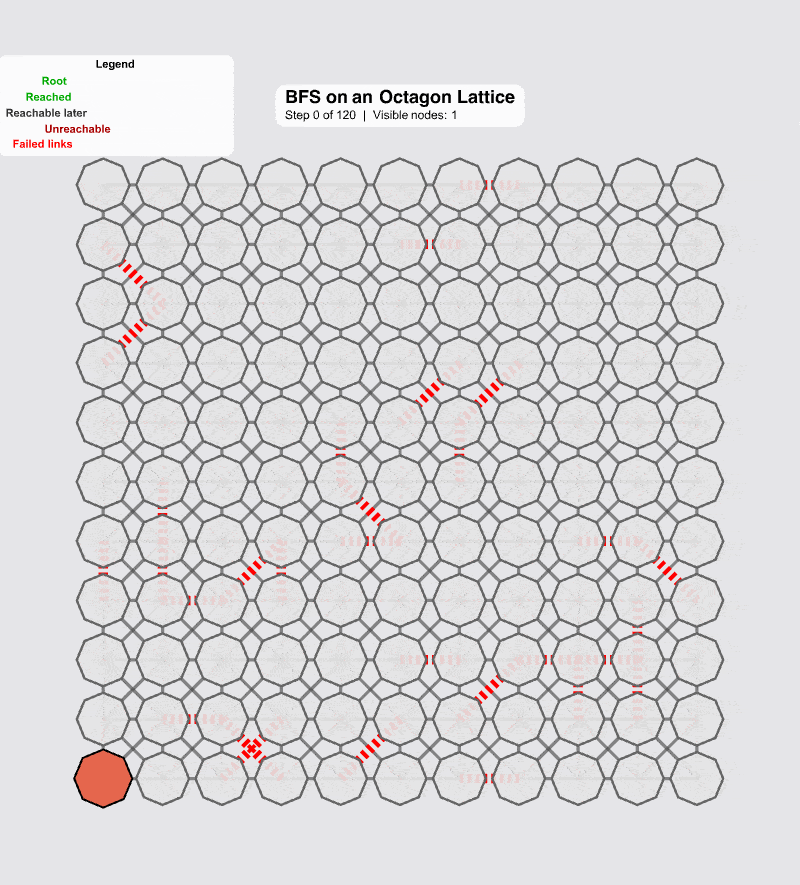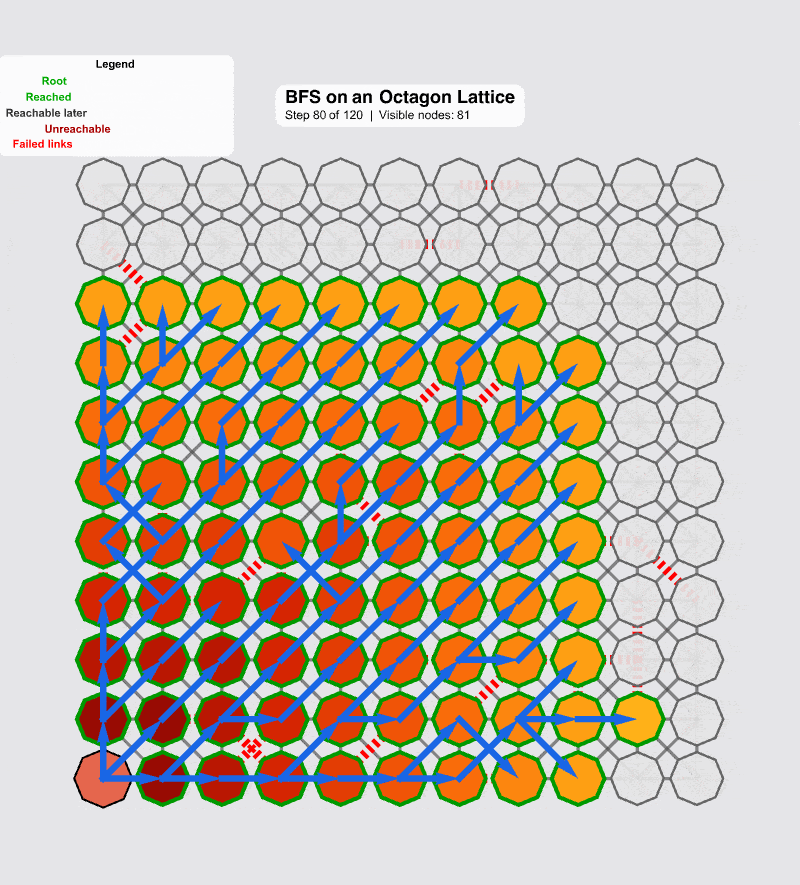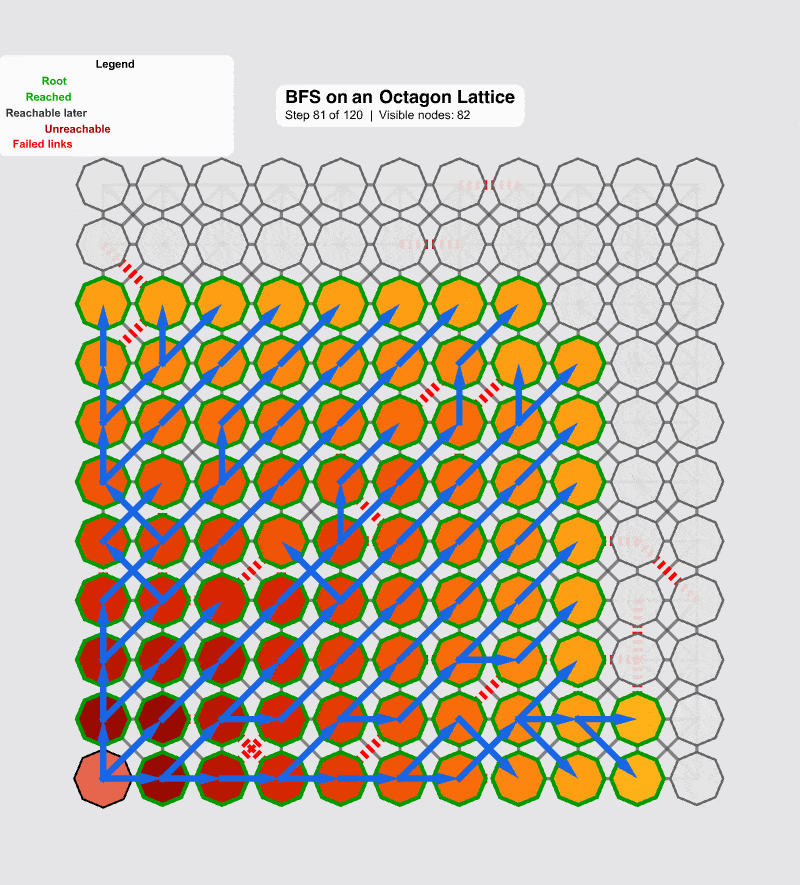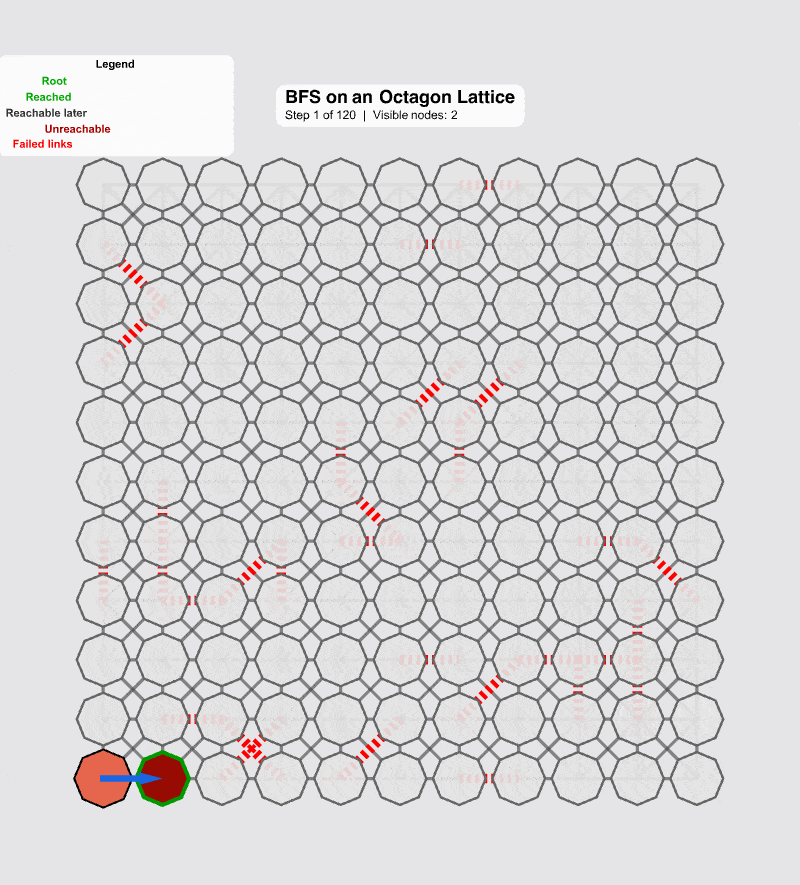
Inset[Framed[
Column[{Style["BFS on an Octagon Lattice", 18, Bold, Black,
FontFamily -> "Helvetica"],
Style[Row[{"Step ", currentStep, " of ", maxSteps,
" | Visible nodes: ", Length[visibleNodes],
" | (Click lattice when paused to step)"}], 12,
GrayLevel[0.05]]}, Spacings -> 0.3],
Background -> Directive[White, Opacity[0.85]],
FrameMargins -> {{10, 10}, {6, 6}}, RoundingRadius -> 10,
FrameStyle ->
Directive[GrayLevel[0.6], Thickness[0.002]]], {Mean[{minX,
maxX}], maxY + 3}],
Inset[Framed[
Grid[{{Style["Legend", 11, Bold,
Black]}, {Row[{Style["Root", 11, Bold, Darker[Green]],
": central red-tinted octagon"}]}, {Row[{Style[
"Reached", 11, Bold, Darker[Green]],
": colored (Solar palette) nodes"}]}, {Row[{Style[
"Reachable later", 11, Bold, GrayLevel[0.2]],
": light gray nodes in component"}]}, {Row[{Style[
"Unreachable", 11, Bold, Darker[Red]],
": pale pink nodes"}]}, {Row[{Style["Failed links", 11,
Bold, Red], ": thick glowing red dashed edges"}]}},
Spacings -> {0.8, 0.6}],
Background -> Directive[White, Opacity[0.85]],
RoundingRadius -> 8, FrameMargins -> {{8, 8}, {6, 6}},
FrameStyle ->
Directive[GrayLevel[0.7], Thickness[0.0015]]], {minX - 4,
maxY + 3}, {Left, Center}]}, ImageSize -> 800,
PlotRange -> {{minX - 3, maxX + 3}, {minY - 3, maxY + 6}},
PlotRangePadding -> Scaled[0.03],
Background -> Lighter[Gray, 0.96]], {"MouseDown" :>
If[! animationRunning && currentStep < maxSteps, currentStep++;]}]]],
Panel[Column[{Style["Network Resilience Metrics", 15, Bold, Black,
FontFamily -> "Helvetica"],
Dynamic[Grid[{{"Total nodes:",
Length[Keys[originalAdjacencyList]]}, {"Total edges:",
Length[allEdges]}, {"Failed edges:",
Length[failedEdges]}, {"Final reachable nodes:",
currentReachable}, {"Final unreachable nodes:",
currentUnreachable}, {"Connectivity:",
If[currentReachable > 0,
Row[{NumberForm[
N[(100.0 currentReachable)/
Length[Keys[originalAdjacencyList]]], {4, 1}], " %"}],
"0 %"]}}, Frame -> All,
Background -> {None, {Lighter[Gray, 0.9], White}},
ItemSize -> All, BaseStyle -> {Black}]]}, Spacings -> 1.2,
BaseStyle -> {Black}],
Background -> Lighter[Blend[{Yellow, White}, 0.8], 0.9],
FrameStyle -> Directive[GrayLevel[0.4], Thickness[0.002]],
FrameMargins -> Medium]}, Spacings -> 1.4]]
Here is a version of the animation starting from the bottom left of the grid, whereas in contrast the centralized version more clearly shows the uniform expansion in a perfectly connected network.
BFS Root Node Diagnostics
Root node: 1 (grid position: {0,0}) with valency: 3
Total edges in graph: 420
The physics suggests that at the tiny micro level, time, from its perspective (frame of reference), can effectively be seen as going backward locally. The direction of time isn't set by some universal clock; it's defined by the flow of information and quantum entanglement between things. It really makes you wonder why there's so many applications like let's say you got a blood transfusion without even checking the Rh factor. Well, it should come as no temporal recurrence that MVCC at scale depends entirely on reliable clock synchronization to detect that right-skew situation. But if the clock sync fails--which we now know it inevitably will at some level of precision--that right-skew goes completely undetected.
The database log, the record of what happened, becomes fundamentally inconsistent, potentially unrecoverable without serious manual intervention--if it's even possible at all. So it's always going to be this way as long as these nodes talk--they pull each other this way and that and even that's all they do but here's a thought experiment--what if you pull a cable?
Modeling: "When You Pull a Cable"
A static, perfect network is a fantasy. A robust system must be designed for failure. As we often say, "an engineer has to learn how to enjoy smoke".
The most critical question is: "When you pull a cable, can it recover all by itself?"
Legacy protocols, built on timeouts, handle this poorly. When a link fails, they enter a "quagmire of timeout and retry", creating ambiguity that leads to "corrupted transactions". Our approach demands that the network knows its state.
The following code comes and creates a continuative simulation. But now, you can use a slider to introduce numFailedEdges--simulating "pulling the cable." When you click "Random Edge Failures," the adjacencyList is up-dated, and the BFS "scouting" algorithm runs again.
And here you shall find something quite weird; the visualization immediately updates (to the extent of that), showing the new, fragmented reality. Nodes that are no longer reachable from the root are obscure and marked as Unreachable.
ClearAll["Global`*"];
rows = 11;
cols = 8;
r = 1.;
gap = 0.2;
dx = 2 r (Cos[\[Pi]/8] + gap);
dy = 2 r (Cos[\[Pi]/8] + gap);
OctagonAt[{x_, y_}, rad_] :=
Polygon[Table[{x, y} +
rad RotationTransform[\[Pi]/8 + (i \[Pi])/4][{1, 0}], {i, 0, 7}]];
idFromIJ[i_Integer, j_Integer] := j cols + i + 1;
ijFromId[id_Integer] := {Mod[id - 1, cols], Quotient[id - 1, cols]};
positions =
Association[
Table[With[{ij = ijFromId[id]},
With[{i = ij[[1]], j = ij[[2]]}, id -> {i dx, j dy}]], {id, 1,
rows cols}]];
adjacencyList =
Association[
Table[Module[{i, j, nbrIJ, nbrIds}, {i, j} = ijFromId[id];
nbrIJ = {{i - 1, j}, {i + 1, j}, {i, j - 1}, {i, j + 1}, {i - 1,
j - 1}, {i + 1, j - 1}, {i - 1, j + 1}, {i + 1, j + 1}};
nbrIds =
idFromIJ @@@
Select[nbrIJ, 0 <= #1[[1]] < cols && 0 <= #1[[2]] < rows &];
id -> nbrIds], {id, 1, rows cols}]];
centerI = Floor[(cols - 1)/2];
centerJ = Floor[(rows - 1)/2];
rootNode = idFromIJ[centerI, centerJ];
Print["Root node (center position ", {centerI, centerJ},
") with valency ", Length[adjacencyList[rootNode]]];
BFS[root_, adj_Association] :=
Module[{dist = Association[root -> 0], q = {root}, current, neigh},
While[q =!= {}, current = First[q]; q = Rest[q];
neigh = adj[current];
Do[If[! KeyExistsQ[dist, v], dist[v] = dist[current] + 1;
q = Append[q, v];], {v, neigh}];]; dist];
distances = BFS[rootNode, adjacencyList];
maxHop = Max[Values[distances]];
hopCounts = Table[Count[Values[distances], h], {h, 0, maxHop}];
cumulativeNodeCounts =
Table[Count[Values[distances], _?(#1 <= h &)], {h, 0, maxHop}];
edgeNodePairs =
Union[Flatten[
Table[Sort /@ Thread[{id, adjacencyList[id]}], {id,
Keys[adjacencyList]}], 1]];
edges = Line /@ (positions /@ #1 &) /@ edgeNodePairs;
Print["Sample edge node pairs: ", Take[edgeNodePairs, UpTo[5]]];
Clear[AccessibleLinksUpToHop];
AccessibleLinksUpToHop[h_Integer?NonNegative] :=
Module[{pairs},
pairs = Select[edgeNodePairs,
With[{u = #1[[1]], v = #1[[2]], du = distances[#1[[1]]],
dv = distances[#1[[2]]]},
du <= h && dv <= h && Min[du, dv] <= h - 1] &]; pairs];
linkCountsAtHop =
Table[Length[AccessibleLinksUpToHop[h]] -
If[h == 0, 0, Length[AccessibleLinksUpToHop[h - 1]]], {h, 0,
maxHop}];
cumulativeLinkCounts =
Table[Length[AccessibleLinksUpToHop[h]], {h, 0, maxHop}];
Print["Hop counts (nodes): ", hopCounts];
Print["Cumulative accessible nodes: ", cumulativeNodeCounts];
Print["New link counts at each hop: ", linkCountsAtHop];
Print["Cumulative accessible links: ", cumulativeLinkCounts];
Print["Links at hop 0: ", cumulativeLinkCounts[[1]]];
If[maxHop >= 1, Print["Links at hop 1: ", cumulativeLinkCounts[[2]]];];
hopColors = {Red, Orange, Yellow, Green, Cyan, Blue, Purple, Pink,
Brown};
CreateGridFrame[currentHop_Integer?NonNegative] :=
Module[{accessibleNodes, linkPairs, linkGraphics, nodeGraphics,
blackLinkCount, pr},
accessibleNodes =
Select[Keys[distances], distances[#1] <= currentHop &];
linkPairs = AccessibleLinksUpToHop[currentHop];
blackLinkCount = Length[linkPairs];
linkGraphics =
Table[If[
MemberQ[linkPairs, edgeNodePairs[[k]]], {Black, Thick,
edges[[k]]}, {LightGray, Thin, edges[[k]]}], {k,
Length[edgeNodePairs]}];
nodeGraphics =
Table[With[{nodeHop = distances[node]},
Module[{color},
color = If[nodeHop <= currentHop,
hopColors[[Mod[nodeHop, Length[hopColors]] + 1]],
LightGray]; {EdgeForm[Black], FaceForm[color],
OctagonAt[positions[node], r]}]], {node, Keys[positions]}];
pr = {{Min[Values[positions][[All, 1]]] - 1.5,
Max[Values[positions][[All, 1]]] +
1.5}, {Min[Values[positions][[All, 2]]] - 1.5,
Max[Values[positions][[All, 2]]] + 1.5}};
Column[{Text[
Style["Hop: " <> ToString[currentHop] <> " | Nodes: " <>
ToString[Length[accessibleNodes]] <> " | Links: " <>
ToString[cumulativeLinkCounts[[currentHop + 1]]] <>
" | Black links: " <> ToString[blackLinkCount], 12, Bold,
Black]],
Graphics[{linkGraphics, nodeGraphics}, ImageSize -> 400,
PlotRange -> pr]}]];
CreateNodeGraphFrame[currentHop_Integer?NonNegative] :=
Module[{hs, currentHopCounts, currentCum}, hs = Range[0, currentHop];
currentHopCounts = hopCounts[[1 ;; currentHop + 1]];
currentCum = cumulativeNodeCounts[[1 ;; currentHop + 1]];
ListLinePlot[{Transpose[{hs, currentHopCounts}],
Transpose[{hs, currentCum}]},
PlotStyle -> {{Red, Thick}, {Blue, Thick}},
PlotLegends -> {"Nodes at each hop", "Cumulative accessible nodes"},
AxesLabel -> {"Hop Count", "Number of Nodes"},
PlotLabel -> "Node Accessibility vs Hop Count",
GridLines -> Automatic, ImageSize -> 400,
PlotRange -> {{0, maxHop}, {0, Max[cumulativeNodeCounts]}}]];
CreateLinkGraphFrame[currentHop_Integer?NonNegative] :=
Module[{hs, currentNew, currentCum}, hs = Range[0, currentHop];
currentNew = linkCountsAtHop[[1 ;; currentHop + 1]];
currentCum = cumulativeLinkCounts[[1 ;; currentHop + 1]];
ListLinePlot[{Transpose[{hs, currentNew}],
Transpose[{hs, currentCum}]},
PlotStyle -> {{Green, Thick}, {Purple, Thick}},
PlotLegends -> {"New links at each hop",
"Cumulative accessible links"},
AxesLabel -> {"Hop Count", "Number of Links"},
PlotLabel -> "Link Accessibility vs Hop Count",
GridLines -> Automatic, ImageSize -> 400,
PlotRange -> {{0, maxHop}, {0, Max[cumulativeLinkCounts]}}]];
animation =
Animate[Column[{Row[{CreateGridFrame[h], Spacer[20],
CreateNodeGraphFrame[h]}], Spacer[10],
CreateLinkGraphFrame[h]}], {h, 0, maxHop, 1}, AnimationRate -> 1,
AnimationDirection -> Forward];
animation
Given all this what's the strictly correct but too-slow baseline? Well, there's one alternative that is 100% reliable: strict two-phase locking. It absolutely guarantees consistency--but it sacrifices performance. You lose the high throughput and low latency that massive web-scale applications demand and that'll do ya.
Root node (center position {3,5}) with valency 8
Sample edge node pairs: {{1,2},{1,9},{1,10},{2,3},{2,9}}
Hop counts (nodes): {1,8,16,24,23,16}
Cumulative accessible nodes: {1,9,25,49,72,88}
New link counts at each hop: {0,8,44,76,87,68}
Cumulative accessible links: {0,8,52,128,215,283}
Links at hop 0: 0
Links at hop 1: 8
So it's this constant trade-off: perfect consistency versus speed. Most modern systems choose speed and simply accept the hidden risk of eventual data corruption due to faulty clocks.
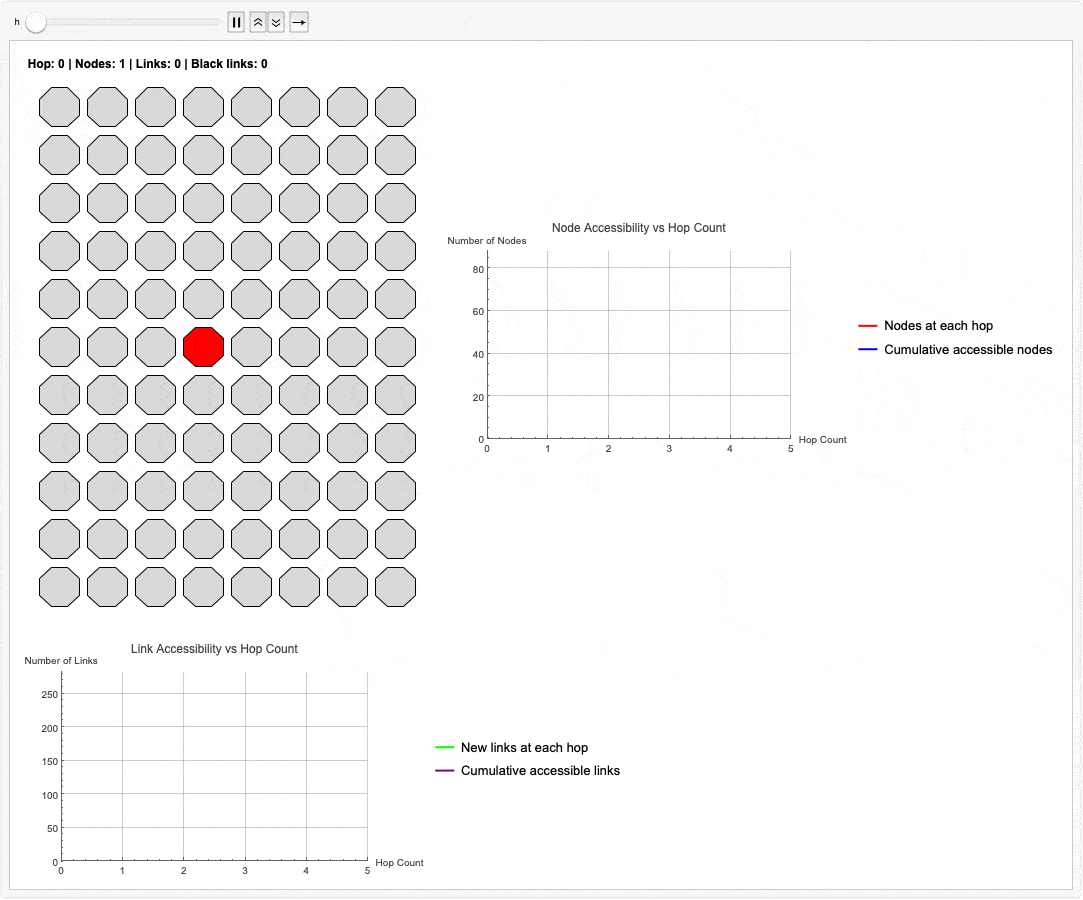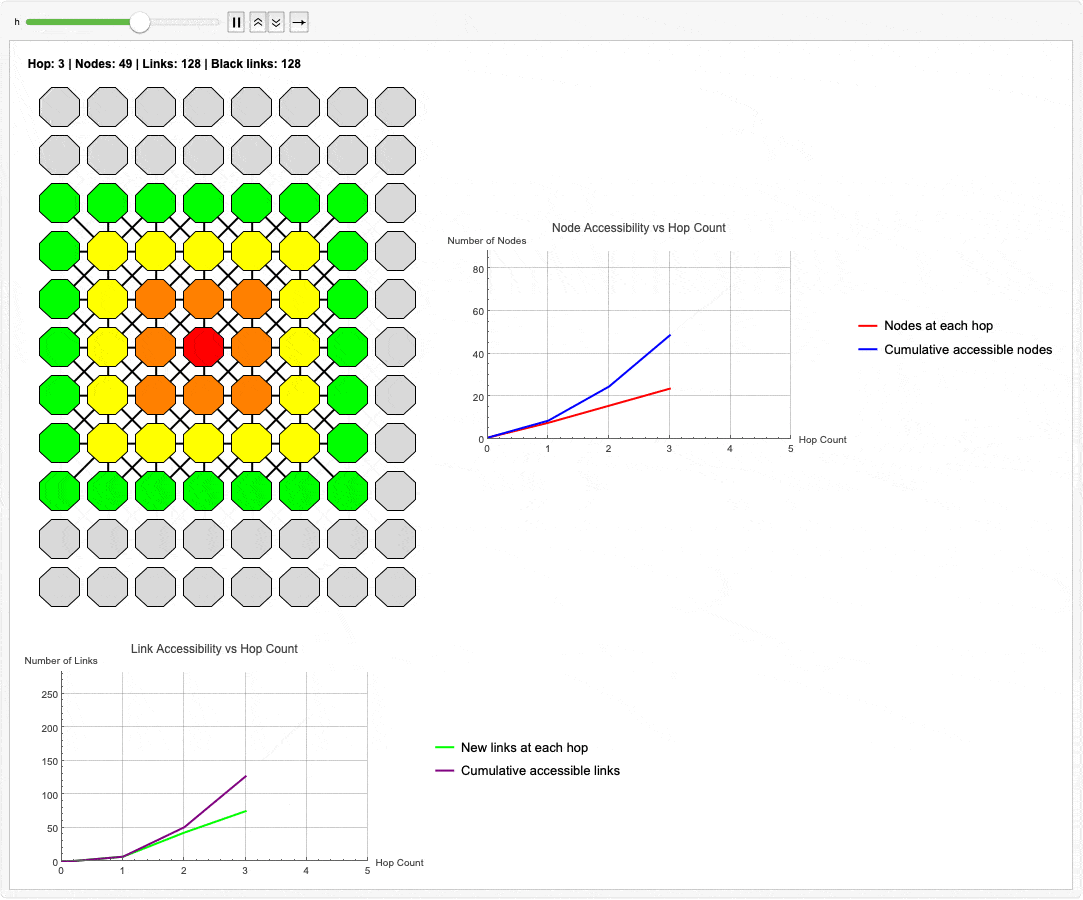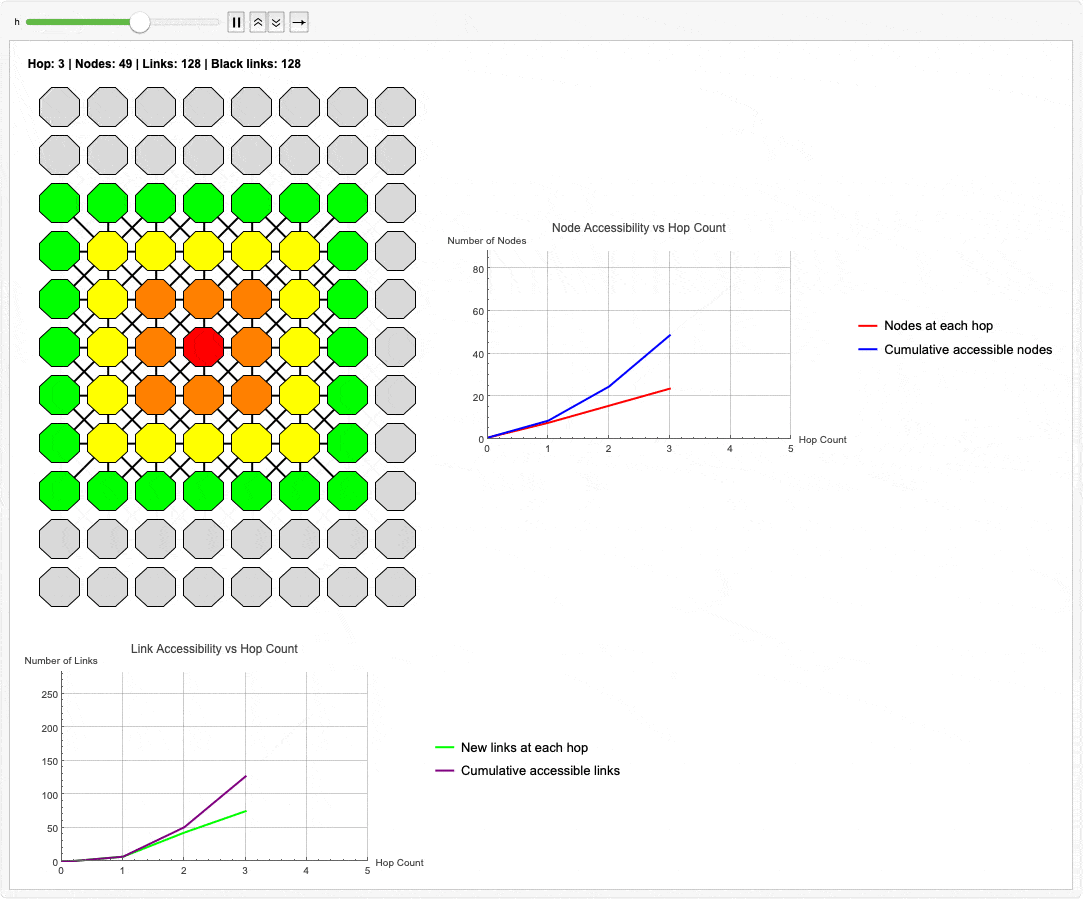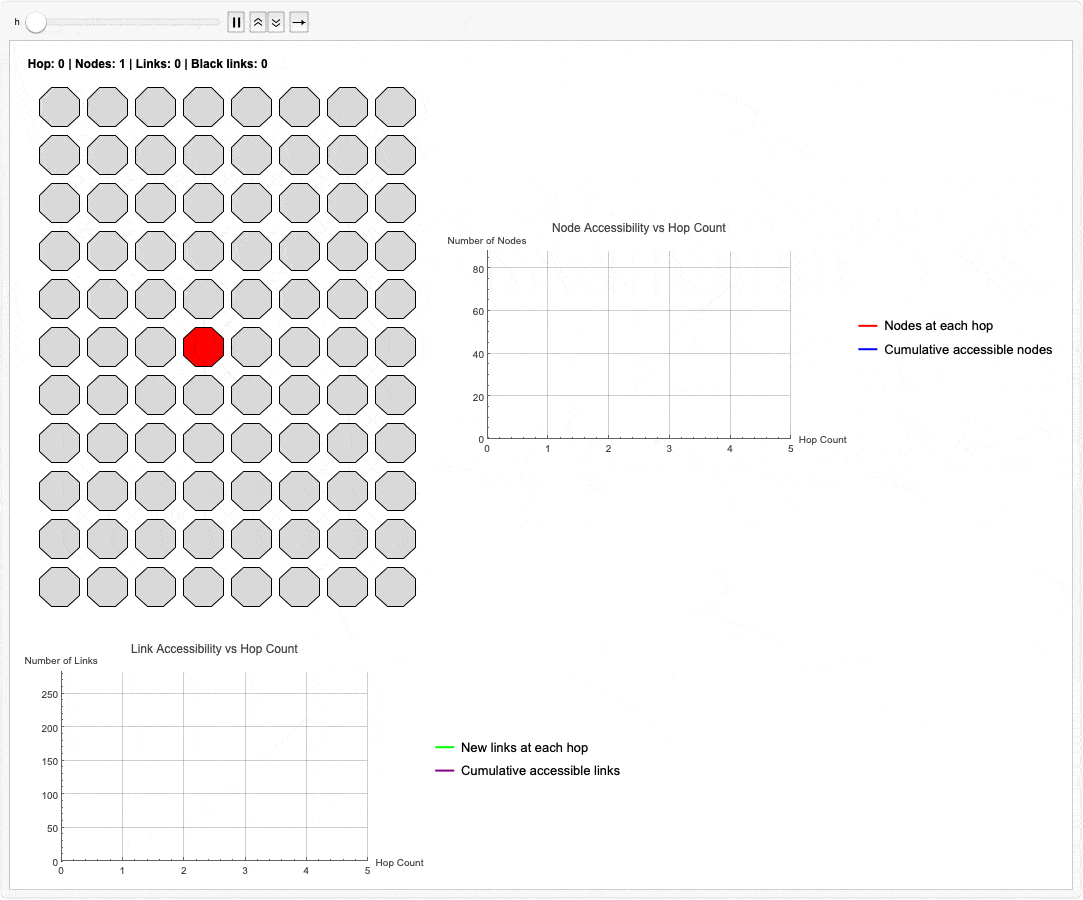
This simulation is the heart of the matter. We have not entered a timeout loop. The graphs don't look like those loops of computational "spaghetti" that plague the ordinary differential topology as we have scouted the new topology. The system knows, with mathematical certainty, that a set of nodes is now unreachable. There is no ambiguity, and therefore, no "right skew" or data corruption. The network has successfully identified the failure and can now "heal around the error"--a process that must happen in nanoseconds, not versus the "milliseconds and seconds" of legacy systems.
ClearAll[rows, cols, r, gap, dx, dy, OctagonAt, positions,
adjacencyList, centerI, centerJ, rootNode, BFS, distances,
GetAccessibleLinksUpToHop, maxHops, hopCounts, cumulativeNodeCounts,
linkCountsAtHop, cumulativeLinkCounts, edgePairsAll, edges,
hopColors, xRange, yRange, CreateGridFrame, CreateNodeGraphFrame,
animation, framesForward, framesLoop];
rows = 11;
cols = 11;
r = 1;
gap = 0.2;
dx = 2 r (Cos[\[Pi]/8] + gap);
dy = 2 r (Cos[\[Pi]/8] + gap);
OctagonAt[{x_, y_}, rr_] :=
Polygon[Table[{x, y} +
rr RotationTransform[\[Pi]/8 + (i \[Pi])/4][{1, 0}], {i, 0, 7}]];
positions = Association[];
Module[{id = 1},
Do[positions[id] = {i dx, j dy};
id++, {j, 0, rows - 1}, {i, 0, cols - 1}];];
adjacencyList = Association[];
Do[Module[{id, neighbors}, id = j cols + i + 1;
neighbors = {{i - 1, j}, {i + 1, j}, {i, j - 1}, {i,
j + 1}, {i - 1, j - 1}, {i + 1, j - 1}, {i - 1, j + 1}, {i + 1,
j + 1}};
adjacencyList[id] =
Reap[Do[With[{ni = neighbor[[1]], nj = neighbor[[2]]},
If[0 <= ni < cols && 0 <= nj < rows,
Sow[nj cols + ni + 1];];], {neighbor, neighbors}]][[2,
1]] /. Null -> {};], {j, 0, rows - 1}, {i, 0, cols - 1}];
centerI = Floor[(cols - 1)/2];
centerJ = Floor[(rows - 1)/2];
rootNode = centerJ cols + centerI + 1;
Print["Root node (center position ", {centerI, centerJ},
") with valency: ", Length[adjacencyList[rootNode]]];
BFS[root_, adjList_Association] :=
Module[{distances, queue, current, neighbors},
distances = Association[root -> 0]; queue = {root};
While[queue =!= {}, current = First[queue]; queue = Rest[queue];
neighbors = adjList[current];
Do[If[! KeyExistsQ[distances, neighbor],
distances[neighbor] = distances[current] + 1;
AppendTo[queue, neighbor];], {neighbor, neighbors}];];
distances];
distances = BFS[rootNode, adjacencyList];
edgePairsAll =
DeleteDuplicates[
Sort /@ Flatten[
Table[Sort[{id, neighbor}], {id, Keys[adjacencyList]}, {neighbor,
adjacencyList[id]}], 1]];
edges = Table[
Line[{positions[pair[[1]]], positions[pair[[2]]]}], {pair,
edgePairsAll}];
Print["Sample edge node pairs: ", Take[edgePairsAll, UpTo[5]]];
GetAccessibleLinksUpToHop[maxHop_Integer] :=
Module[{accessibleLinks},
accessibleLinks =
Select[edgePairsAll,
Function[{pair},
With[{u = pair[[1]], v = pair[[2]], uDist = distances[pair[[1]]],
vDist = distances[pair[[2]]]},
uDist <= maxHop && vDist <= maxHop &&
Min[uDist, vDist] <= maxHop - 1]]]; accessibleLinks];
maxHops = Max[Values[distances]] + 1;
hopCounts = Table[Count[Values[distances], h], {h, 0, maxHops}];
cumulativeNodeCounts =
Table[Count[Values[distances], x_ /; x <= h], {h, 0, maxHops}];
linkCountsAtHop =
Table[Module[{currentLinks, previousLinks},
currentLinks = GetAccessibleLinksUpToHop[h];
previousLinks = If[h > 0, GetAccessibleLinksUpToHop[h - 1], {}];
Length[currentLinks] - Length[previousLinks]], {h, 0, maxHops}];
cumulativeLinkCounts =
Table[Length[GetAccessibleLinksUpToHop[h]], {h, 0, maxHops}];
Print["Hop counts (nodes): ", hopCounts];
Print["Cumulative accessible nodes: ", cumulativeNodeCounts];
Print["New link counts at each hop: ", linkCountsAtHop];
Print["Cumulative accessible links: ", cumulativeLinkCounts];
Print["Links at hop 0: ", Length[GetAccessibleLinksUpToHop[0]]];
Print["Links at hop 1: ", Length[GetAccessibleLinksUpToHop[1]]];
xRange = {Min[Values[positions][[All, 1]]] - 1.5,
Max[Values[positions][[All, 1]]] + 1.5};
yRange = {Min[Values[positions][[All, 2]]] - 1.5,
Max[Values[positions][[All, 2]]] + 1.5};
hopColors = {Red, Orange, Yellow, Green, Cyan, Blue, Purple, Pink,
Brown};
CreateGridFrame[currentHop_Integer] :=
Module[{accessibleNodes, accessibleLinkPairs, linkGraphics,
blackLinkCount, nodeGraphics},
accessibleNodes =
Select[Keys[distances], distances[#1] <= currentHop &];
accessibleLinkPairs = GetAccessibleLinksUpToHop[currentHop];
linkGraphics =
MapThread[
If[MemberQ[accessibleLinkPairs, #2], {Black,
Thick, #1}, {LightGray, Thin, #1}] &, {edges, edgePairsAll}];
blackLinkCount = Count[linkGraphics, {Black, Thick, _}];
nodeGraphics =
Table[Module[{nodeHop, color}, nodeHop = distances[node];
color = If[nodeHop <= currentHop,
hopColors[[Mod[nodeHop, Length[hopColors]] + 1]],
LightGray]; {EdgeForm[Black], FaceForm[color],
OctagonAt[positions[node], r]}], {node, Keys[positions]}];
Column[{Text[
Style["Hop: " <> ToString[currentHop] <>
" | Accessible Nodes: " <> ToString[Length[accessibleNodes]] <>
" | Accessible Links: " <>
ToString[cumulativeLinkCounts[[currentHop + 1]]] <>
" | Black Links: " <> ToString[blackLinkCount],
FontSize -> 12, FontWeight -> Bold, Black]],
Graphics[{linkGraphics, nodeGraphics}, ImageSize -> 400,
PlotRange -> {xRange, yRange}, Background -> White]}]];
CreateNodeGraphFrame[currentHop_Integer] :=
Module[{hopRange, currentCumulativeNodes, currentCumulativeLinks},
hopRange = Range[0, currentHop];
currentCumulativeNodes = cumulativeNodeCounts[[1 ;; currentHop + 1]];
currentCumulativeLinks =
cumulativeLinkCounts[[1 ;; currentHop + 1]];
ListLinePlot[{Transpose[{hopRange, currentCumulativeLinks}],
Transpose[{hopRange, currentCumulativeNodes}]},
PlotStyle -> {{Red, Thick}, {Blue, Thick}},
PlotLegends -> {"Cumulative accessible links",
"Cumulative accessible nodes"},
AxesLabel -> {"Hop count", "Count"},
PlotLabel -> "Cumulative Accessibility vs Hop Count",
GridLines -> Automatic, ImageSize -> 400, Joined -> True,
PlotRange -> {{0, maxHops}, {0,
4 (rows - 1) (cols - 1) + rows + cols - 2}}]];
animation =
Animate[Row[{CreateGridFrame[h], Spacer[20],
CreateNodeGraphFrame[h]}], {h, 0, maxHops, 1},
AnimationRate -> 1, AnimationDirection -> Forward];
framesForward =
Table[Row[{CreateGridFrame[h], Spacer[20],
CreateNodeGraphFrame[h]}], {h, 0, maxHops}];
framesLoop = Join[framesForward, Rest[Most[Reverse[framesForward]]]];
Export["hopLinks3_pingpong.gif", framesLoop,
"DisplayDurations" -> 0.6, "AnimationRepetitions" -> \[Infinity]];
ListAnimate[framesLoop];
animation
The process of "discovery and pathfinding"
Root node (center position {5,5}) with valency: 8
Sample edge node pairs: {{1,2},{1,12},{1,13},{2,3},{2,13}}
Hop counts (nodes): {1,8,16,24,32,40,0}
Cumulative accessible nodes: {1,9,25,49,81,121,121}
New link counts at each hop: {0,8,44,76,108,140,44}
Cumulative accessible links: {0,8,52,128,236,376,420}
Links at hop 0: 0
Links at hop 1: 8
This Wolfram Language model is more than a computer science demonstration. I couldn't believe what I was modeling--a physically-grounded network. By starting with a "ground up" definition of the physical mesh and running a "scouting" algorithm, we can prove inside-out the network's properties.
Most importantly, by simulating failure, we demonstrate how a network built on discovery--rather than the "flawed assumption" of universal time--can achieve true resilience, unambiguously identifying "unreachable" components and "making the world safe for transactions".
Since we can't fix time, the goal here is to achieve something they call logically instantaneous. The only way to truly get the effect of logical simultaneity is to essentially engineer time out of the equation for critical operations. One can go from any time-limited, API between computational models designed to simulate the resilience and discovery properties of a "mesh-based network" topology without needing to know the implementation language for the entire simulation and analysis. But if that's not something that you can really do, a primary feature being to generate animated GIFs and plots to show the "BFS" Wavefront Expansion", then what I would describe as good for the visualization and analysis of a network lattice, its adjacencies, and its properties, could be building an analysis of hop counts as a node-accessible application of discrete mathematics and graph theory. Which grounds the entire premise of the network in the failure of modern systems to account for fundamental physics, such as the "Minkowski fallacy". As well as the "discovery and pathfinding" for a new network architecture, which is a fundamental engineering problem and makes it possible to directly apply computer science concepts..specifically graph theory and network algorithms (BFS) in our simulations.
ClearAll["Global`*"];
rows = 11;
cols = 11;
r = 1;
gap = 0.2;
dx = 2 r (Cos[\[Pi]/8] + gap);
dy = 2 r (Cos[\[Pi]/8] + gap);
OctagonAt[{x_, y_}, rad_] :=
Polygon[Table[{x, y} +
rad RotationTransform[\[Pi]/8 + (i \[Pi])/4][{1, 0}], {i, 0, 7}]];
positions =
Association[
Flatten[Table[
With[{id = j cols + i + 1}, id -> {i dx, j dy}], {j, 0,
rows - 1}, {i, 0, cols - 1}], 1]];
adjacencyList =
Association[
Flatten[Table[
With[{id = j cols + i + 1},
Module[{nbrIdx, validNbrs},
nbrIdx = {{i - 1, j}, {i + 1, j}, {i, j - 1}, {i,
j + 1}, {i - 1, j - 1}, {i + 1, j - 1}, {i - 1,
j + 1}, {i + 1, j + 1}};
validNbrs =
Select[nbrIdx, 0 <= #1[[1]] < cols && 0 <= #1[[2]] < rows &];
id -> (validNbrs /. {ii_, jj_} :> jj cols + ii + 1)]], {j, 0,
rows - 1}, {i, 0, cols - 1}], 1]];
centerI = Floor[cols/2];
centerJ = Floor[rows/2];
rootNode = centerJ cols + centerI + 1;
Print[Style[
Row[{"Root node: (center position: ", {centerI, centerJ},
") with valency: ", Length[adjacencyList[rootNode]]}], 14, Bold]];
invalidEdges = RandomInteger[50, 60];
BFS[root_, adj_Association] :=
Module[{distances, queue, current, neighbors},
distances = Association[root -> 0]; queue = {root};
While[queue =!= {}, current = First[queue]; queue = Rest[queue];
neighbors = adj[current];
Do[If[! KeyExistsQ[distances, nbr],
distances[nbr] = distances[current] + 1;
queue = Append[queue, nbr];], {nbr, neighbors}];]; distances];
distances = BFS[rootNode, adjacencyList];
maxHops = Max[Values[distances]];
GetAccessibleLinksUpToHop[maxHop_Integer] :=
Module[{accessibleLinks}, accessibleLinks = {};
Do[Do[Module[{linkPair, uDist, vDist},
linkPair = Sort[{node, neighbor}];
If[! MemberQ[accessibleLinks, linkPair], uDist = distances[node];
vDist = distances[neighbor];
If[uDist <= maxHop && vDist <= maxHop &&
Min[uDist, vDist] <= maxHop - 1,
AppendTo[accessibleLinks, linkPair];];];], {neighbor,
adjacencyList[node]}], {node, Keys[adjacencyList]}];
accessibleLinks];
hopCounts = Table[Count[Values[distances], h], {h, 0, maxHops}];
cumulativeNodeCounts =
Table[Count[Values[distances], x_ /; x <= h], {h, 0, maxHops}];
linkCountsAtHop =
Table[Module[{currentLinks, previousLinks},
currentLinks = GetAccessibleLinksUpToHop[h];
previousLinks = If[h > 0, GetAccessibleLinksUpToHop[h - 1], {}];
Length[currentLinks] - Length[previousLinks]], {h, 0, maxHops}];
cumulativeLinkCounts =
Table[Length[GetAccessibleLinksUpToHop[h]], {h, 0, maxHops}];
Print["Hop counts (nodes): ", hopCounts];
Print["Cumulative accessible nodes: ", cumulativeNodeCounts];
Print["New link counts at each hop: ", linkCountsAtHop];
Print["Cumulative accessible links: ", cumulativeLinkCounts];
Print["Links at hop 0: ", Length[GetAccessibleLinksUpToHop[0]]];
Print["Links at hop 1: ", Length[GetAccessibleLinksUpToHop[1]]];
edges = {};
edgeToNodePair = {};
Do[Do[Module[{edgeLine, nodePair},
edgeLine = Line[{positions[id], positions[neighbor]}];
nodePair = Sort[{id, neighbor}]; AppendTo[edges, edgeLine];
AppendTo[edgeToNodePair, nodePair];], {neighbor,
adjacencyList[id]}], {id, Keys[adjacencyList]}];
uniqueEdges = {};
uniqueNodePairs = {};
Do[If[! MemberQ[uniqueNodePairs, edgeToNodePair[[i]]],
AppendTo[uniqueEdges, edges[[i]]];
AppendTo[uniqueNodePairs, edgeToNodePair[[i]]];], {i, Length[edges]}];
edges = uniqueEdges;
edgeToNodePair = uniqueNodePairs;
Print["Sample edge node pairs: ", Take[edgeToNodePair, 5]];
hopPalette[hop_, maxHop_] :=
ColorData["DarkRainbow"][Rescale[hop, {0, maxHop}]];
posArray = Values[positions];
{xMin, xMax} = MinMax[posArray[[All, 1]]];
{yMin, yMax} = MinMax[posArray[[All, 2]]];
plotRange2D = {{xMin - 1.5, xMax + 1.5}, {yMin - 1.5, yMax + 1.5}};
maxRange = 4 (rows - 1) (cols - 1) + rows + cols - 2;
CreateGridFrame[currentHop_Integer] :=
Module[{accessibleNodes, accessibleLinkPairs, linkGraphics,
nodeGraphics, blackLinkCount},
accessibleNodes =
Select[Keys[distances], distances[#1] <= currentHop &];
accessibleLinkPairs = GetAccessibleLinksUpToHop[currentHop];
linkGraphics =
Table[Module[{pair = edgeToNodePair[[i]], base = edges[[i]],
styleActive, styleInactive},
styleActive =
Directive[ColorData["BrightBands"][0.15], Opacity[0.9],
Thickness[0.006]];
styleInactive =
Directive[GrayLevel[0.4], Opacity[0.2], Thickness[0.002]];
If[MemberQ[accessibleLinkPairs, pair], {styleActive,
base}, {styleInactive, base}]], {i, Length[edges]}];
blackLinkCount = Length[accessibleLinkPairs];
nodeGraphics =
Table[Module[{nodeHop, col, baseStyle, inactiveStyle},
nodeHop = distances[node]; col = hopPalette[nodeHop, maxHops];
baseStyle = {EdgeForm[{GrayLevel[0.05], Thickness[0.003]}],
Glow[Directive[col, Opacity[0.85]]],
FaceForm[Directive[col, Opacity[0.95]]]};
inactiveStyle = {EdgeForm[{GrayLevel[0.2], Thickness[0.0015]}],
FaceForm[Directive[GrayLevel[0.35], Opacity[0.25]]]};
If[nodeHop <= currentHop, {baseStyle,
OctagonAt[positions[node], r]}, {inactiveStyle,
OctagonAt[positions[node], r]}]], {node, Keys[positions]}];
Column[{Style[
Row[{"Hop: ", currentHop, " | Accessible Nodes: ",
Length[accessibleNodes], " | Accessible Links: ",
cumulativeLinkCounts[[currentHop + 1]],
" | Active Links This Frame: ", blackLinkCount}], 13,
Black, Bold],
Graphics[{{Directive[GrayLevel[0.95], Opacity[1]],
Rectangle[{xMin - 2, yMin - 2}, {xMax + 2, yMax + 2}]},
linkGraphics,
nodeGraphics, {Directive[Black, Thickness[0.006], Opacity[0.9]],
Circle[positions[rootNode], 1.15 r]}}, Background -> White,
PlotRange -> plotRange2D, ImageSize -> 420, Frame -> True,
FrameStyle -> Directive[GrayLevel[0.3], Thickness[0.002]],
PlotRangePadding -> Scaled[0.05]]}]];
CreateNodeGraphFrame[currentHop_Integer] :=
Module[{currentHopCounts, currentCumulativeNodes,
currentCumulativeLinks, dataLinks, dataNodes},
currentHopCounts = hopCounts[[1 ;; currentHop + 1]];
currentCumulativeNodes = cumulativeNodeCounts[[1 ;; currentHop + 1]];
currentCumulativeLinks =
cumulativeLinkCounts[[1 ;; currentHop + 1]];
dataLinks =
Transpose[{Range[0, currentHop], currentCumulativeLinks}];
dataNodes =
Transpose[{Range[0, currentHop], currentCumulativeNodes}];
ListLinePlot[{dataLinks, dataNodes},
PlotStyle -> {Directive[ColorData["BrightBands"][0.2], Thick],
Directive[ColorData["BrightBands"][0.7], Thick, Dashed]},
PlotMarkers -> {{Automatic, 4}, {Automatic, 4}}, Frame -> True,
FrameLabel -> {Style["Hop Count", 13, GrayLevel[0.2]],
Style["Cumulative Count", 13, GrayLevel[0.2]]},
PlotLabel ->
Style["Accessibility vs. Hop Distance", 14, Bold, Black],
GridLines -> {Range[0, maxHops, 2], None},
GridLinesStyle ->
Directive[GrayLevel[0.8], Dashed, Thickness[0.0015]],
Background -> White,
FrameStyle -> Directive[GrayLevel[0.3], Thickness[0.002]],
TicksStyle -> Directive[GrayLevel[0.2], 10],
PlotRange -> {{0, maxHops}, {0, maxRange}}, ImageSize -> 420,
PlotRangePadding -> Scaled[0.05],
PlotLegends ->
Placed[{"Cumulative accessible links",
"Cumulative accessible nodes"}, {0.55, 0.9}]]];
frames =
Table[Row[{CreateGridFrame[h], Spacer[20], CreateNodeGraphFrame[h]},
ImageSize -> 900], {h, 0, maxHops}];
animation =
Animate[Row[{CreateGridFrame[h], Spacer[20], CreateNodeGraphFrame[h]},
ImageSize -> 900], {h, 0, maxHops, 1}, AnimationRate -> 1,
AnimationDirection -> Forward, DefaultDuration -> maxHops + 1];
ListAnimate[frames];
Export["hopLinks_sidebyside_beautiful.gif", frames,
"DisplayDurations" -> 1];
animation
For "scouting" a "mesh-based network topology", this is something I can definitely see--how a node in a "sea of XPUs" can perform "local discovery" to build a map of its environment based on hop-count, not on a "flawed assumption" about universal time; the essential first step before any "routing" can occur.
Root node: (center position: {5,5}) with valency: 8
Hop counts (nodes): {1,8,16,24,32,40}
Cumulative accessible nodes: {1,9,25,49,81,121}
New link counts at each hop: {0,8,44,76,108,140}
Cumulative accessible links: {0,8,52,128,236,376}
Links at hop 0: 0
Links at hop 1: 8
Sample edge node pairs: {{1,2},{1,12},{1,13},{2,3},{2,13}}
Lattice and Topology Definition
This section sets up the physical and logical structure of our network. We define an 11x11 grid of octagonal nodes, representing a "sea of XPUs". The adjacencyList defines the "mesh-based network topology" by connecting each node to its 8 nearest neighbors, a sturdy design that means (engineering time out of the critical path) either freezing time locally for long enough, or shrinking the physical distance down so much that you can process a batch of related events consistently before time drift or communication delays matter.
The Scouting Algorithm (BFS)
Out of the pile of all nodes we select a rootNode (the center of the grid) to begin the "scouting" process. We use a Breadth-First Search (BFS) to simulate the "discovery and pathfinding". The BFS algorithm expands hop by hop, discovering the network's topology.
The output, distances, is an Association that maps every reachable node ID to its hop-count from the root. This map is the "coordinate system", built organically from connectivity, completely avoiding the "Minkowski fallacy" of assuming a universal clock.
Temporal intimacy and the Æthernet link
This starts with physically engineering something called temporal intimacy. The servers must be physically close enough for extremely reliable low-latency interaction. You use extremely short cables--just a few inches long--connecting adjacent machines directly in a dense mesh topology. You are literally fighting physics with hardware layout. And so it falls out--the Æthernet link is designed to be bidirectionally coherent. It's not about node A sending a message and node B maybe sending an acknowledgement later.
With the distances map, we can now analyze the network's properties. We gather data on how many nodes and links are discovered at each successive hop. This is vital for "modeling trade-offs and resource allocation", the network accessibility that allows an engineer to understand the cost (in hops) of reaching any part of the network.

This scouting wavefront, builds the animation; CreateGridFrame generates the left panel, the "BFS Wavefront Expansion". It iterates through currentHop, coloring the nodes and links as they are "discovered" by the scouting algorithm. For our purposes, CreateNodeGraphFrame generates the right panel, plotting the "Accessibility vs. Hop Distance". This graph shows the cumulative growth of the known network, illustrating how cumulativeLinkCounts and cumulativeNodeCounts expand with each hop.
These exported GIF(s) show the "scouting" process in action, the routes of all "discovery and pathfinding for a mesh-based network'.
rows = 11;
cols = 11;
r = 1;
gap = 0.2;
dx = 2 r (Cos[\[Pi]/8] + gap);
dy = 2 r (Cos[\[Pi]/8] + gap);
OctagonAt[{x_, y_}, rr_] :=
Polygon[Table[{x, y} +
rr RotationTransform[\[Pi]/8 + (i \[Pi])/4][{1, 0}], {i, 0, 7}]];
positions = Association[];
Module[{id = 1},
Do[positions[id] = {i dx, j dy};
id++, {j, 0, rows - 1}, {i, 0, cols - 1}];];
originalAdjacencyList = Association[];
Do[Module[{id, neighbors}, id = j cols + i + 1;
originalAdjacencyList[id] = {};
neighbors = {{i - 1, j}, {i + 1, j}, {i, j - 1}, {i,
j + 1}, {i - 1, j - 1}, {i + 1, j - 1}, {i - 1, j + 1}, {i + 1,
j + 1}};
Do[Module[{ni = neighbor[[1]], nj = neighbor[[2]], nid},
If[0 <= ni < cols && 0 <= nj < rows, nid = nj cols + ni + 1;
AppendTo[originalAdjacencyList[id], nid];];], {neighbor,
neighbors}];], {j, 0, rows - 1}, {i, 0, cols - 1}];
centerI = 0;
centerJ = 0;
rootNode = centerJ cols + centerI + 1;
Print[Style[
Row[{"Root node: ", rootNode,
" (grid position: ", {centerI, centerJ}, ") valency: ",
Length[originalAdjacencyList[rootNode]]}], 14, Bold, Black]];
allEdges = {};
Do[Do[If[id < neighbor,
AppendTo[allEdges, {id, neighbor}];], {neighbor,
originalAdjacencyList[id]}], {id, Keys[originalAdjacencyList]}];
Print[Style[Row[{"Total edges in graph: ", Length[allEdges]}], 12,
Bold, Black]];
RemoveEdges[adjList_Association, edgesToRemove_List] :=
Module[{newAdjList = Association[adjList]},
Do[Module[{u = edge[[1]], v = edge[[2]]},
newAdjList[u] = DeleteCases[newAdjList[u], v];
newAdjList[v] = DeleteCases[newAdjList[v], u];], {edge,
edgesToRemove}]; newAdjList];
AnimatedBFS[root_, adjList_Association] :=
Module[{distances, parentMap, queue, current, neighbors, steps},
distances = Association[root -> 0]; parentMap = Association[];
queue = {root}; steps = {Association[distances]};
While[queue =!= {}, current = First[queue]; queue = Rest[queue];
neighbors = Lookup[adjList, current, {}];
Do[If[! KeyExistsQ[distances, neighbor],
distances[neighbor] = distances[current] + 1;
parentMap[neighbor] = current; AppendTo[queue, neighbor];
AppendTo[steps, Association[distances]];], {neighbor,
neighbors}];]; {distances, parentMap, steps}];
DynamicModule[{numFailedEdges = 0, failedEdges = {},
currentReachable = Length[Keys[originalAdjacencyList]],
currentUnreachable = 0, finalDistances = Association[],
finalParentMap = Association[], bfsSteps = {},
currentAdjList = originalAdjacencyList,
maxFailures = Min[50, Length[allEdges]], animationRunning = False,
currentStep = 0, maxSteps = 0,
animationSpeed = 0.5}, {finalDistances, finalParentMap, bfsSteps} =
AnimatedBFS[rootNode, currentAdjList];
currentReachable = Length[Keys[finalDistances]];
currentUnreachable =
Length[Keys[originalAdjacencyList]] - currentReachable;
maxSteps = Max[0, Length[bfsSteps] - 1];
Column[{Panel[
Column[{Style["Network Failure & BFS Controls", 16, Bold, Black,
FontFamily -> "Helvetica"],
Row[{"Number of failed edges: ",
Slider[Dynamic[numFailedEdges], {0, Length[allEdges], 1}],
Spacer[8],
Panel[Dynamic[numFailedEdges], Background -> White,
FrameMargins -> {{6, 6}, {2, 2}}]}],
Row[{"Animation speed (seconds/step): ",
Slider[Dynamic[animationSpeed], {0.1, 2.0, 0.1}], Spacer[8],
Dynamic[Style[NumberForm[animationSpeed, {2, 1}], 12, Black]]}],
Row[{Style["Reachable nodes: ", Bold, Darker[Green]],
Dynamic[currentReachable], Spacer[20],
Style["Unreachable nodes: ", Bold, Darker[Red]],
Dynamic[currentUnreachable]}],
Row[{Button[Style["Random Edge Failures", 12, Bold, Black],
failedEdges =
If[numFailedEdges > 0,
RandomSample[allEdges, numFailedEdges], {}];
currentAdjList =
RemoveEdges[originalAdjacencyList,
failedEdges]; {finalDistances, finalParentMap, bfsSteps} =
AnimatedBFS[rootNode, currentAdjList];
currentReachable = Length[Keys[finalDistances]];
currentUnreachable =
Length[Keys[originalAdjacencyList]] - currentReachable;
maxSteps = Max[0, Length[bfsSteps] - 1]; currentStep = 0;
animationRunning = False;], Spacer[10],
Button[Style["Start BFS Animation", 12, Bold, Black],
If[Length[bfsSteps] > 0, currentStep = 0;
animationRunning = True;];], Spacer[10],
Button[Style["Reset All Links", 12, Bold, Black],
failedEdges = {}; numFailedEdges = 0;
currentAdjList =
originalAdjacencyList; {finalDistances, finalParentMap,
bfsSteps} = AnimatedBFS[rootNode, currentAdjList];
currentReachable = Length[Keys[finalDistances]];
currentUnreachable = 0;
maxSteps = Max[0, Length[bfsSteps] - 1]; currentStep = 0;
animationRunning = False;]}],
If[maxSteps > 0,
Row[{"Animation step: ",
Slider[Dynamic[currentStep], {0, maxSteps, 1}], Spacer[6],
Dynamic[Style[Row[{currentStep, " / ", maxSteps}], 11, Bold,
Black]]}], Nothing]}, Spacings -> 1.2, BaseStyle -> {Black}],
Background -> Lighter[Blend[{Gray, Blue}, 0.15], 0.85],
FrameMargins -> Medium,
FrameStyle -> Directive[GrayLevel[0.4], Thickness[0.003]]],
Dynamic[If[animationRunning && currentStep < maxSteps,
Pause[animationSpeed]; currentStep++;
If[currentStep >= maxSteps, animationRunning = False];]; ""],
Dynamic[Module[{workingEdges, workingCoords, failedCoords,
failedEdgeLines, workingEdgeLines, nodeGraphics, arrowGraphics,
currentDistancesStep, visibleNodes, coords, minX, maxX, minY,
maxY, maxKnownDist, distanceColor},
currentDistancesStep =
If[Length[bfsSteps] > 0 && 0 <= currentStep < Length[bfsSteps],
bfsSteps[[currentStep + 1]], Association[]];
visibleNodes = Keys[currentDistancesStep];
workingEdges = Complement[allEdges, failedEdges];
workingCoords = (positions /@ #1 &) /@ workingEdges;
failedCoords = (positions /@ #1 &) /@ failedEdges;
coords =
Values[positions]; {minX, maxX} = {Min[coords[[All, 1]]],
Max[coords[[All, 1]]]}; {minY, maxY} = {Min[coords[[All, 2]]],
Max[coords[[All, 2]]]};
maxKnownDist =
If[finalDistances === Association[], 1,
Max[Values[finalDistances]]];
distanceColor[d_] :=
ColorData["SolarColors"][Rescale[d, {0, maxKnownDist}, {0, 1}]];
failedEdgeLines =
If[failedCoords === {}, {}, {Glow[Red],
Directive[Red, Thickness[0.012], Dashed, CapForm["Round"]],
Line /@ failedCoords}];
workingEdgeLines =
If[workingCoords === {}, {}, {Directive[GrayLevel[0.25, 0.7],
Thickness[0.004]], CapForm["Round"], Line /@ workingCoords}];
nodeGraphics =
Table[Module[{pt = positions[node]},
Which[node === rootNode, {EdgeForm[{Black, Thick}],
FaceForm[RGBColor[0.95, 0.55, 0.35]], OctagonAt[pt, 1.1 r]},
MemberQ[visibleNodes,
node], {EdgeForm[{Darker[Green, 0.4], Thickness[0.005]}],
FaceForm[distanceColor[currentDistancesStep[node]]],
OctagonAt[pt, r]},
KeyExistsQ[finalDistances,
node], {EdgeForm[{GrayLevel[0.4], Thickness[0.003]}],
FaceForm[Directive[GrayLevel[0.92], Opacity[0.95]]],
OctagonAt[pt, r]},
True, {EdgeForm[{GrayLevel[0.7], Thickness[0.002]}],
FaceForm[Directive[RGBColor[0.93, 0.8, 0.88], Opacity[0.7]]],
OctagonAt[pt, r]}]], {node, Keys[positions]}];
arrowGraphics =
If[finalParentMap === Association[], {},
Table[If[
KeyExistsQ[finalParentMap, node] &&
MemberQ[visibleNodes, node], {Directive[
RGBColor[0.15, 0.45, 0.95], Thickness[0.008]],
Arrowheads[0.03],
Arrow[{positions[finalParentMap[node]], positions[node]}]},
Nothing], {node, Keys[finalParentMap]}]];
Graphics[{{FaceForm[Lighter[Blend[{Blue, Black}, 0.9], 0.9]],
EdgeForm[None],
Rectangle[{minX - 10, minY - 10}, {maxX + 10, maxY + 10}]},
workingEdgeLines, failedEdgeLines, nodeGraphics, arrowGraphics,
Inset[Framed[
Column[{Style["BFS on an Octagon Lattice", 18, Bold, Black,
FontFamily -> "Helvetica"],
Style[Row[{"Step ", currentStep, " of ", maxSteps,
" | Visible nodes: ", Length[visibleNodes]}], 12,
GrayLevel[0.1]]}, Spacings -> 0.3],
Background -> Directive[White, Opacity[0.9]],
FrameMargins -> {{10, 10}, {6, 6}}, RoundingRadius -> 10,
FrameStyle ->
Directive[GrayLevel[0.6], Thickness[0.002]]], {Mean[{minX,
maxX}], maxY + 3}],
Inset[Framed[
Grid[{{Style["Legend", 11, Bold,
Black]}, {Row[{Style["Root", 11, Bold, Darker[Green]],
": central orange octagon"}]}, {Row[{Style["Reached",
11, Bold, Darker[Green]],
": Solar-colored nodes"}]}, {Row[{Style[
"Reachable later", 11, Bold, GrayLevel[0.25]],
": light gray nodes"}]}, {Row[{Style["Unreachable", 11,
Bold, Darker[Red]],
": pale pink nodes"}]}, {Row[{Style["Failed links", 11,
Bold, Red], ": thick glowing red dashed edges"}]}},
Spacings -> {0.8, 0.6}],
Background -> Directive[White, Opacity[0.9]],
RoundingRadius -> 8, FrameMargins -> {{8, 8}, {6, 6}},
FrameStyle ->
Directive[GrayLevel[0.7], Thickness[0.0015]]], {minX - 4,
maxY + 3}, {Left, Center}]}, ImageSize -> 800,
PlotRange -> {{minX - 3, maxX + 3}, {minY - 3, maxY + 6}},
PlotRangePadding -> Scaled[0.03],
Background -> Lighter[Gray, 0.96]]]],
Panel[Column[{Style["Network Resilience Analysis", 15, Bold, Black,
FontFamily -> "Helvetica"],
Dynamic[Grid[{{"Total Nodes:",
Length[Keys[originalAdjacencyList]]}, {"Total Edges:",
Length[allEdges]}, {"Failed Edges:",
Length[failedEdges]}, {"Final Reachable Nodes:",
currentReachable}, {"Final Unreachable Nodes:",
currentUnreachable}, {"Connectivity:",
If[currentReachable > 0,
Row[{NumberForm[
N[(100.0 currentReachable)/
Length[Keys[originalAdjacencyList]]], {4, 1}], " %"}],
"0 %"]}}, Frame -> All,
Background -> {None, {Lighter[Gray, 0.9], White}},
ItemSize -> All, BaseStyle -> {Black}]]}, Spacings -> 1.2],
Background -> Lighter[Blend[{Yellow, White}, 0.8], 0.9],
FrameStyle -> Directive[GrayLevel[0.4], Thickness[0.002]],
FrameMargins -> Medium]}, Spacings -> 1.4]]
The Æthernet link is designed to be bidirectionally coherent. It's not about node A sending a message and node B maybe sending an acknowledgement later. It's about..nothing other than guaranteeing that whatever relevant state change happens on one side of that short wire happens effectively simultaneously and reliably on the other side, without relying on software timers or sequence numbers.
They describe it as spacetime having a handshake--an architecture that physically and logically correlates events across that link faster and more reliably than clock synchronization could ever hope to achieve.
Hardware causal registers at the boundary
The final piece thoroughly involves putting complex causal registers directly into the smart NIC, right next to the wire. This is really the linchpin of the design, putting the intelligence right there at the network boundary. These registers are specifically designed to detect and potentially migrate those tricky right-skew conflicts at the hardware level, almost instantaneously, as the data flows across the link.
It's a direct engineering solution to the physics problem of time that has gradually plagued distributed systems for decades.
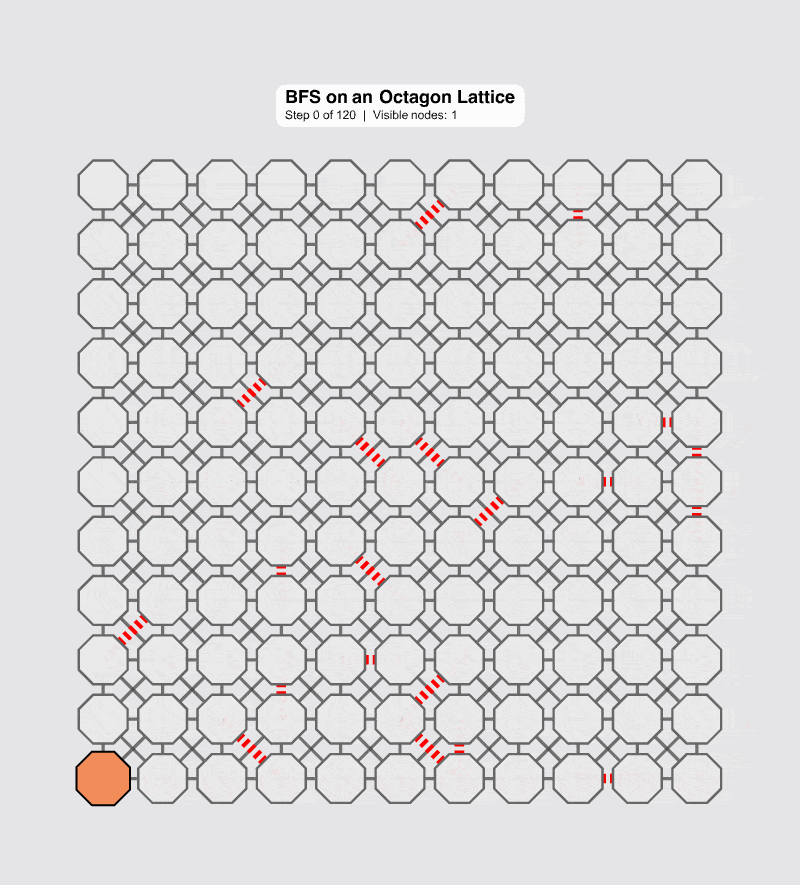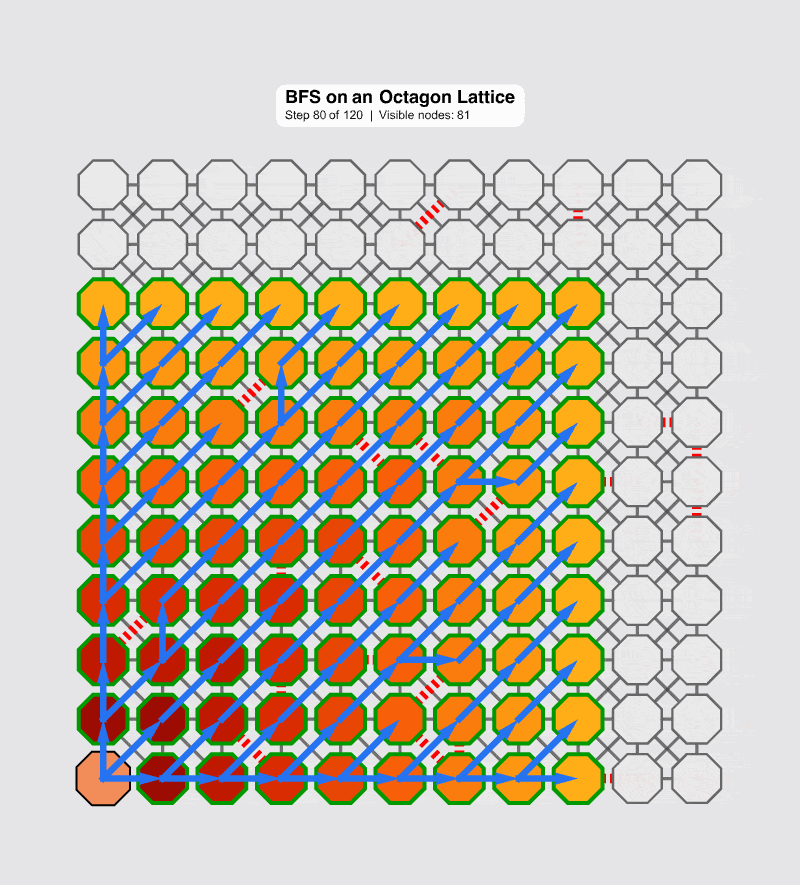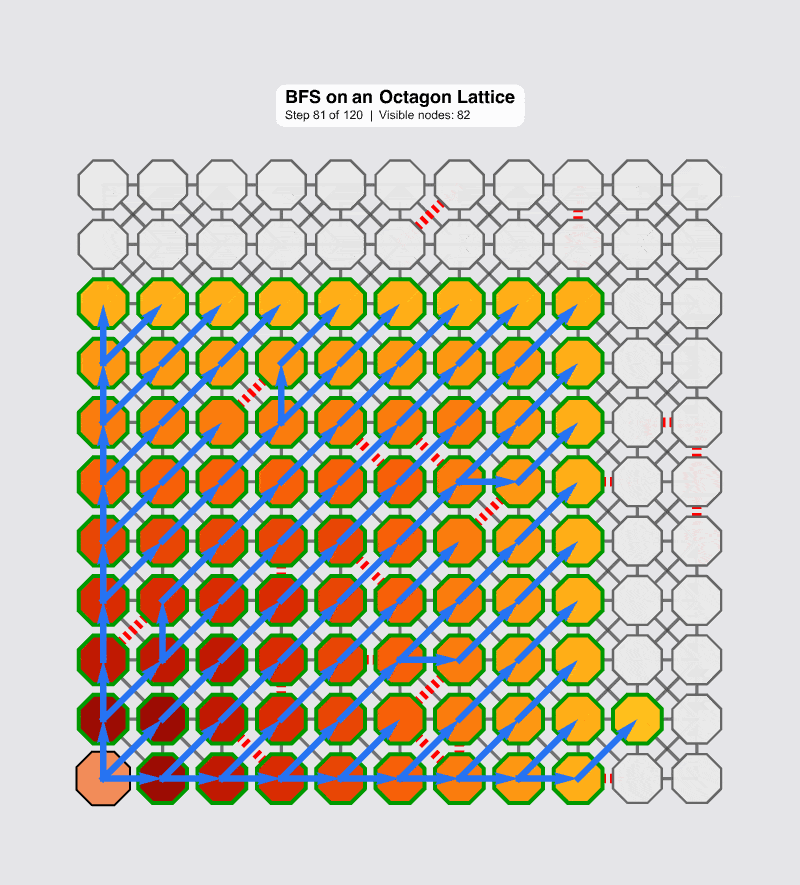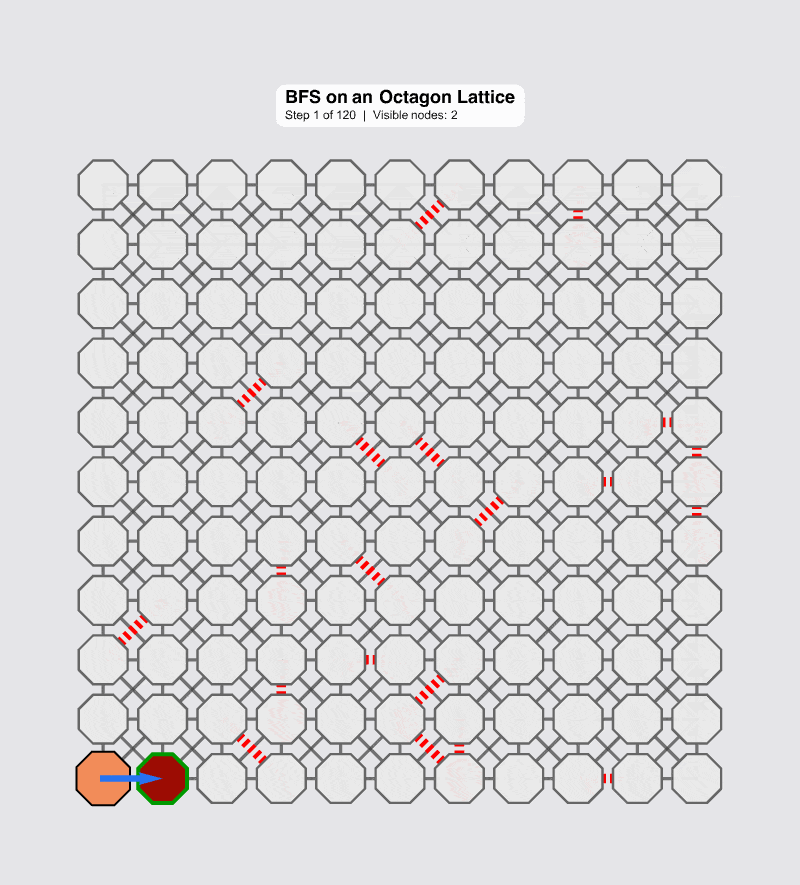
Closing perspective
We're finally starting to build serviceable systems that actually acknowledge the true, fragmented, localized, and frankly weird nature of time. If concepts we take for granted--like happened-before and point-in-time--are actually meaningless without also specifying a point in space, what practical assumptions are you still relying on every day that are really just comforting illusions about the simple, universal nature of time? And so we've picked up on how the earlier Cloud Sync / Lamport material forms a single, coherent basis for "logically instantaneous causality versus timestamp illusions".