Greetings to my fellow Mathematica users!
I'm an amateur user of Mathematica and I'm currently facing some trouble with modelling of a planar region which is described by 3 x-y coordinates and a curved line represented by an equation. I tried my best in coming up with the illustration below to show what I mean:
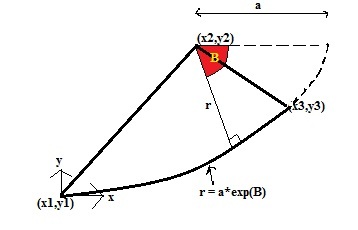 <-- Description of Planar region
<-- Description of Planar region
- B = Angle between Horizontal (at x2,y2) and the line described by r
- r = Equation of the curve region, described by: r = a*exp(B)
- a = Value of r when B = 0
- (x,y) = Coordinates of the vertices
Is Mathematica able to model such a region defined by 3 coordinates and an equation? I'm bordering on the edge of frustration in trying to look for the way to create this region in Mathematica. I would really be grateful if someone could point me in the right direction of defining such a region.
Thank you in advance and have a great day!
Regards Corse