Hi Cook,
Thank you for your guidance. After studying your paper, I discovered that your theory aligns remarkably well with my simulation data, providing the theoretical backing for the deviations I previously observed.
My initial value of 133 was a baseline derived solely from the Average Degree. Based on your framework, I applied a correction using the following parameters:
Dimensional Gradient: Since the dimension is not uniform throughout the model (the internal Bulk dimension is greater than the Boundary), I utilized the average dimension within the 20%-90% radial scaling zone.
Regarding your mention of the 'Shadow Filter', I realized that my implementation of the Interaction Ratio correction performs exactly this function. It captures the 'return flux' from the collision events, which successfully bridged the gap from the bare 133 value to the convergent 136-138 range.
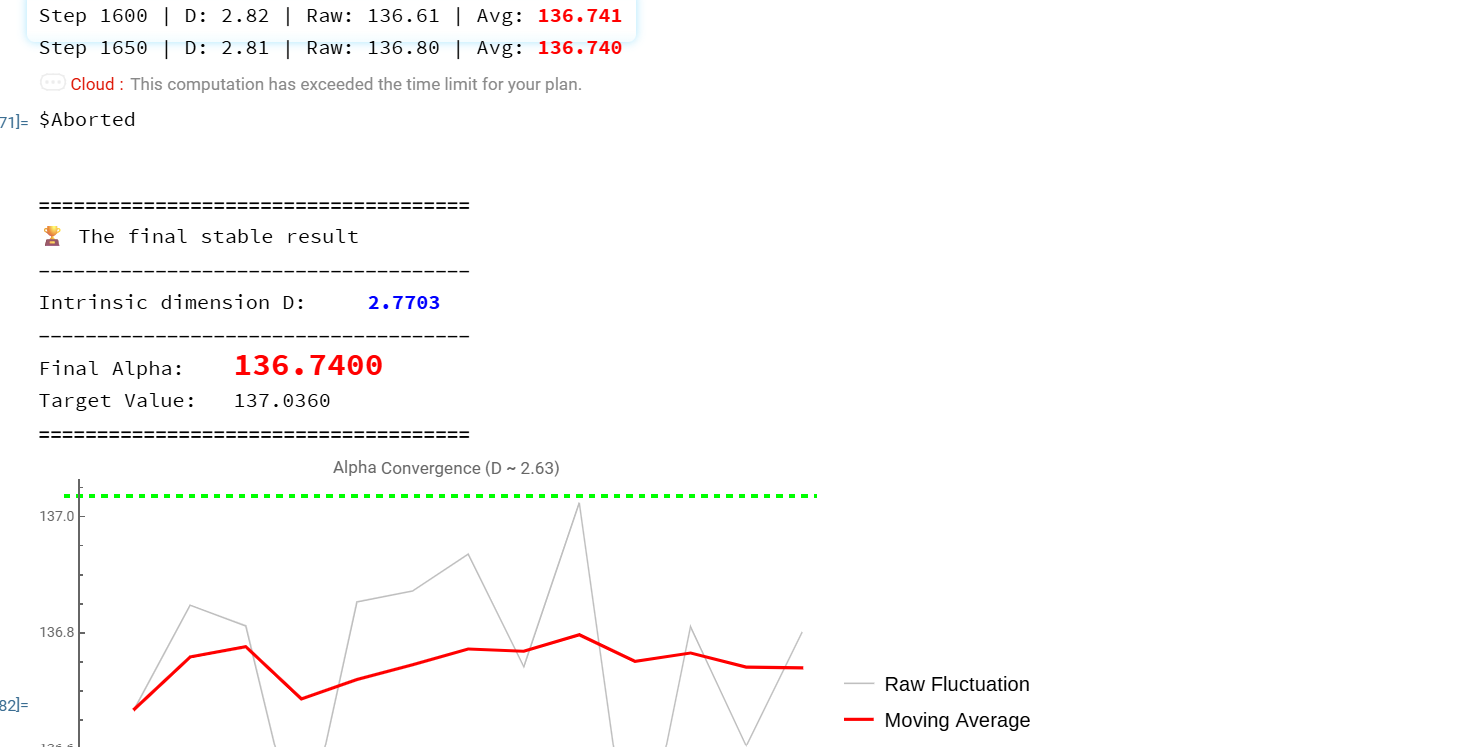
The result is promising (as shown in the attached figure): The corrected value now fluctuates around 136.8.
Regarding the fluctuations seen in the average dimension graph, I attribute this to the discrete nature of my observation method and the topological dynamics:
Observation Method: To prevent computational deadlocks from parallel processing, I adopted a "snapshot-per-node-birth" approach.
Node Role Differentiation: Each new node plays a distinct topological role—some serve as Bulk Fillers, while others act as Boundary Expanders.
This alternation of roles causes instantaneous jumps in the dimension per step, but it has little impact on the statistical mean. As previously noted, the effective constant stabilizes robustly in the 136 - 138 range.
Regarding Gravitational Waves: As for your insights regarding Gravitational Waves and the dispersion relation, I want to dedicate more time to fully digest Section 19 to ensure I grasp the implications for my lattice structure. I will follow up on this specific topic as soon as possible!
 Best regards,
Best regards,
 Attachments:
Attachments: