I'm solving a linearized ODE (to study accretion flow in a disk)
ar = NDSolve[{D[F[t, l]^-1*l^7, t] == D[D[F[t, l], l], l], F[t, 50] == 2, F[t, .001] == 0, F[0, l] == Sigma4[l]},
F, {t, 0, 1000}, {l, .001, 10}]; br= Plot3D[Evaluate[F[t, l] /. ar], {t, 0, 1000}, {l, .001, 5}]
where
Sigma4[r_] :=
Piecewise[{{1 + Cos[Pi (r^.5 - 2)], 1 < r < 4}, {2, r >= 4}, {0, r <= 1}}]
is the initial condition, which looks like
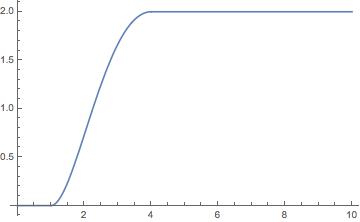
I take a time t=0 slice of the 3D solution to my function ar
Plot[Evaluate[F[0, l] /. ar], {l, 0.001, 10}, PlotRange -> All]
which yields
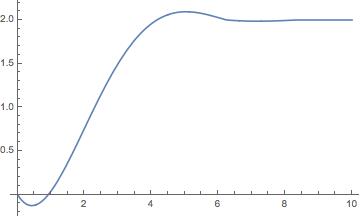
This is different from my imposed initial condition. I played with my function ar, and realized that for
ar2 = NDSolve[{D[F[t, l], t] == D[D[F[t, l], l], l], F[t, 50] == 2, F[t, .001] == 0, F[0, l] == Sigma4[l]},
F, {t, 0, 1000}, {l, .001, 10}]
the initial condition is satisfied.
I'm guessing a singularity in the solution causes the warping of my initial condition. How can I regain the initial condition for my function ar? Perhaps there is a way to give more weight to it?