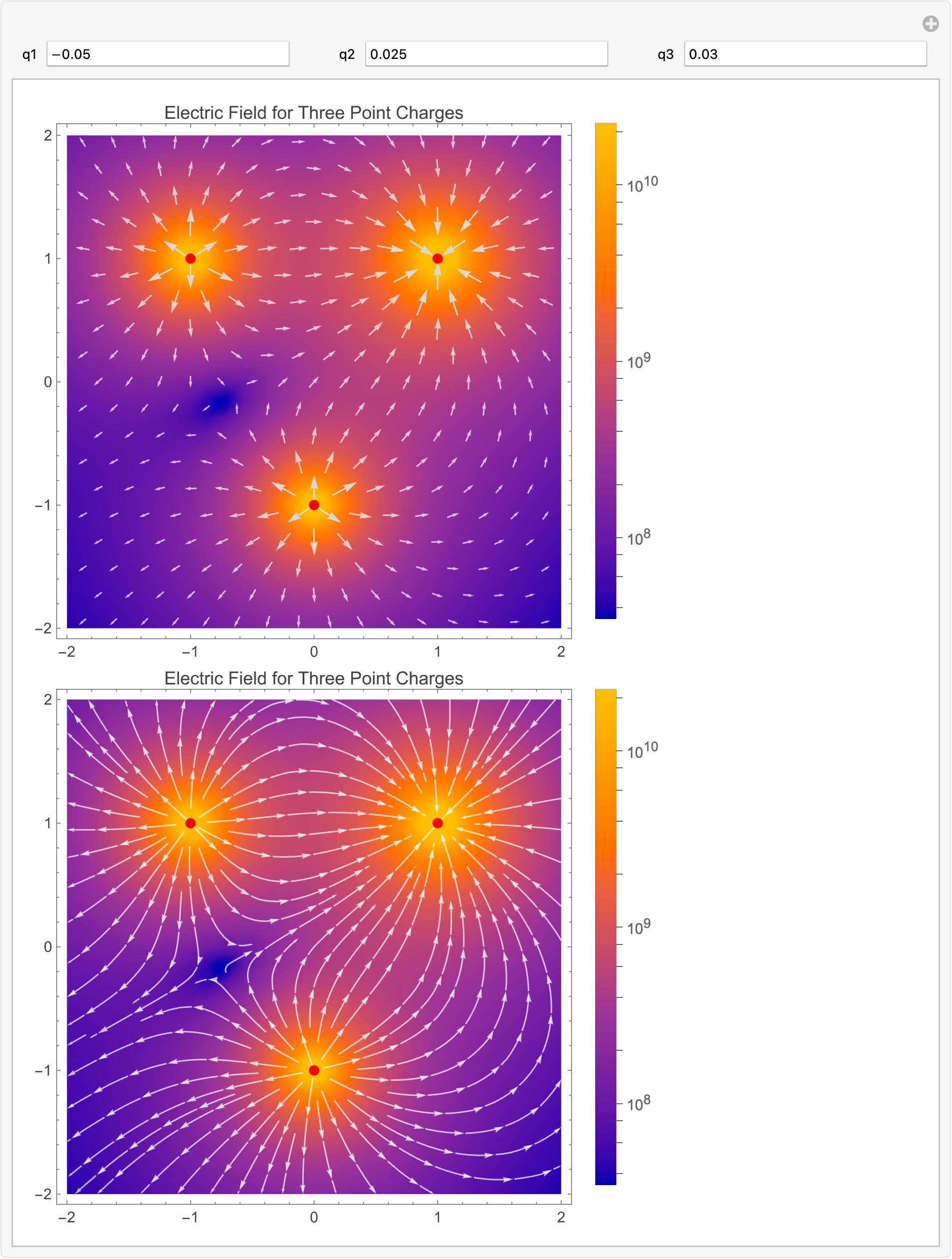
A different style, with the log of the field intensity as a background (just to give another idea about visualization; plus it was a bit harder to code than I thought it would be):
ClearAll[x, y, logTicks];
logTicks[{min_, max_}] := Replace[
Range[Floor[min], Ceiling[max]],
t1_List :>
Join[{#, 10^HoldForm[#]} & /@ t1,
Flatten[Table[{# + Log10@k, ""}, {k, 2, 8, 2}] & /@ Most@t1, 1]]
];
Manipulate[
Module[{norm, q, field, \[Epsilon]₀(*,format*)(*,normRange*)},
norm[vec_] := Sqrt[Total[vec^2]];
q := {{q1, {1, 1}}, {q2, {0, -1}}, {q3, {-1, 1}}};
\[Epsilon]₀ = 8.85418782 10^-12;
field = 1/(4 \[Pi] \[Epsilon]₀ ) \!\(
\*UnderoverscriptBox[\(\[Sum]\), \(i = 1\), \(3\)]
\*FractionBox[\(q[[i, 1]]\ \(({x, y} - q[[i, 2]])\)\),
SuperscriptBox[\(norm[{x, y} - q[[i, 2]]]\), \(3\)]]\);
With[(* a bunch of nested With[]s *)
{vplot = Reap[
VectorPlot[field
, {x, -2, 2}, {y, -2, 2}
, VectorScaling -> Automatic
, VectorColorFunction -> (GrayLevel[1., 0.7] &)
, EvaluationMonitor :>(* sow norms to get range (below) *)
Sow[Norm@field, "norm"]]
, "norm"],
splot = StreamPlot[field
, {x, -2, 2}, {y, -2, 2}
, StreamColorFunction -> (GrayLevel[1., 0.7] &)
]},
{normRange = With[{
bound = Block[{x, y},
Max@Table[(* upper bound from offset of charged points *)
{x, y} = q[[i, 2]] + {0.1, 0.1}; Norm[field]
, {i, 3}]]},
Log10@Clip[MinMax@{Last@vplot, bound}, {bound/10000., bound}]
]},
{scf =
ColorDataFunction["WL12DefaultVectorGradient",
"ThemeGradients", {0, 1},
Blend["WL12DefaultVectorGradient", #1] & ][
Rescale[#1, normRange]] &},
{leg = BarLegend[{scf, normRange}
, ColorFunctionScaling -> False
, Ticks -> logTicks[normRange]]},
{format = {PlotLabel -> "Electric Field for Three Point Charges"
, PlotLegends -> leg
, Epilog -> {Red, PointSize[0.02`],
Table[Point[q[[i, 2]]], {i, 1, Length[q]}]}
, ImageSize -> Medium}},
{fieldStrength = DensityPlot[Norm@field, {x, -2, 2}, {y, -2, 2}
, ColorFunctionScaling -> False
, ColorFunction -> Function[{n}, scf[Clip[Log10@n, normRange]]]
, PlotRange -> All
, format (* needed only here b/c of Show[] *)
]},
Column[
{Show[fieldStrength, First@vplot, PlotLegends -> leg],
Show[fieldStrength, splot, PlotLegends -> leg
]}
]
]],
Row[
{Control[{{q1, -0.05}, ControlType -> InputField}], Spacer[30],
Control[{{q2, 0.025}, ControlType -> InputField}], Spacer[30],
Control[{{q3, 0.03}, ControlType -> InputField}]}],
TrackedSymbols :> Manipulate]