Group Abstract Group Abstract

Message Boards Message Boards

0
|
87 Views
|
3 Replies
|
3 Total Likes
View groups...
Share
Share this post:

How to transform identically for factors to include the specified partial form?

Bill Blair
Posted 8 days ago 
eqn = -4 a^2 b^2 (-b^2 + (b^4 x0^2)/(
    a^2 y0^2) - (-((b^2 x0^2)/(a^2 y0)) + y0)^2)

How to perform an identical transformation on the above expression into a factored form containing the specified part? The specific target form of the transformation is shown in the figure below:

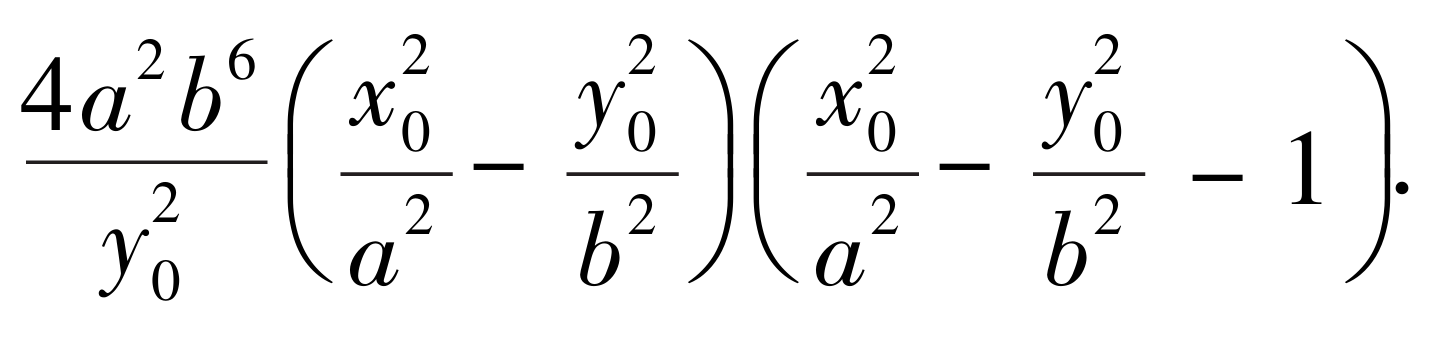
enter image description here

The specified contained part is:

(x0^2/a^2 - y0^2/b^2)

I have conducted the following independent attempts yet been unable to resolve this issue.

pol = -4 a^2 b^2 (-b^2 + (b^4 x0^2)/(
    a^2 y0^2) - (-((b^2 x0^2)/(a^2 y0)) + y0)^2)
pol/(x0^2/a^2 - y0^2/b^2) // Cancel // Factor
POSTED BY: Bill Blair
3 Replies
Sort By: 
Factor[
  eqn /. {x0 -> Sqrt[u] a, y0 -> Sqrt[w] b}
  ] /. ({u -> x0^2/a^2, w -> y0^2/b^2})
(*  (4 a^2 b^6 (-1 + x0^2/a^2 - y0^2/b^2) (x0^2/a^2 - y0^2/b^2))/y0^2  *)

Also:

sub = {x0 == a Sqrt[u], y0 == b Sqrt[w]};
Factor[
  eqn /. First@Solve[sub, {x0, y0}]
  ] /. First@Normal@Quiet@Solve[sub, {u, w}]
POSTED BY: Michael Rogers

Solve based approach

eqn = -4 a^2 b^2 (-b^2 + (b^4 x0^2)/(a^2 y0^2) - \
(-((b^2 x0^2)/(a^2 y0)) + y0)^2)
expr = (x0^2/a^2 - y0^2/b^2)
Factor[(eqn /. Solve[k == expr, x0][[1]])] /. k -> expr
POSTED BY: Bruno Tenorio

Here is a way that uses FactorList:

eqn = -4 a^2 b^2 (-b^2 +
     (b^4 x0^2)/(a^2 y0^2) -
     (-((b^2 x0^2)/(a^2 y0)) +
        y0)^2);
expr = (x0^2/a^2 - y0^2/b^2);
FactorList[eqn/expr]
% /. {c_Plus, 1} :>
  Splice@{{a^2 b^2, 1},
    {Expand[c/(a^2 b^2)], 1}}
MapApply[Power, %]
expr*Times @@ %
POSTED BY: Gianluca Gorni
Reply to this discussion
Community posts can be styled and formatted using the Markdown syntax.
Tag limit exceeded
Note: Only the first five people you tag will receive an email notification; the other tagged names will appear as links to their profiles.
Reply Preview
Attachments
Remove
or Discard