Wolfram Language(WL) provides several useful interfaces to link itself to libraries written in other language. NETLink and JLink are such very powerful tools that bridge WL to the strong objective-oriented languages. I am going to show briefly an example about how to call a NuGet library for C sharp from WL.

http://www.mathdotnet.com/ is a project on NuGet that promotes the numerical computing power of C sharp. It does lots of things like what BLAS and LAPACK does for linear algebra and numeric solvers. Of course Mathematica and MATLAB(R) are much more mature products than this library. I use this library simply to show how you can call an external library.

I am writing this example with Mathematica 10 + Windows 7 + Visual Studio 2012.

1. Follow this link http://numerics.mathdotnet.com/ to install the MathNet assembly into any open project or clone the git drive
2. You can locate the assembly on your machine by right-clicking the entry in Solution Explorer (VS 2012): reference->MathNet.Numeric->Properties

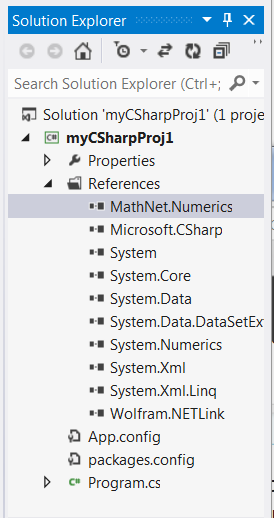
Now you can open Mathematica and load the .NETLink package.

Needs["NETLink`"]

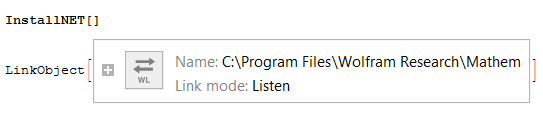
You can launch the runtime link connection with

InstallNET[]

Assume things are going well, here is what you see:

If you have targeted the location of MathNet.Numerics.dll in your project, you can load the assembly with LoadNETAssembly

LoadNETAssembly["MathNet.Numerics","C:\\Users\\shenghui\\...myCSharpProj1\\packages\\MathNet.Numerics.3.2.3\\lib\\net40\\"]

Of course your absolute path may be different, here it is just my location to store the dll file. As in the VS2012, you have a xml tree about the build-in classes and objects in this MathNet package:

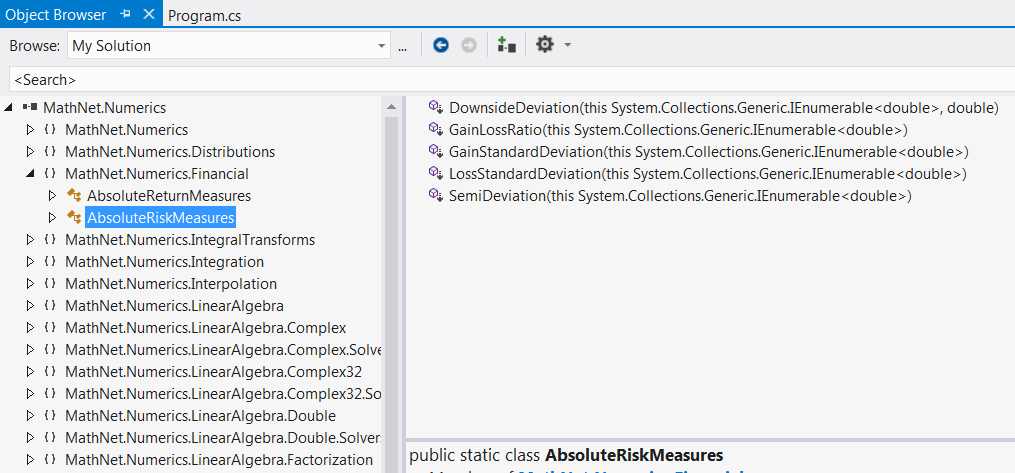
The same view can be generated within Mathematica by NETTypeInfo function:

http://numerics.mathdotnet.com/docs/ provides the following example code ( Using's are omitted ):

Matrix<double> A = DenseMatrix.OfArray(new double[,] {
        {1,1,1,1},
        {1,2,3,4},
        {4,3,2,1}});
Vector<double>[] nullspace = A.Kernel();

This is where Mathematica has to call a different method. The Vector generic type is valid and can be loaded into Mathematica without problem:

In:= netType=LoadNETType["MathNet.Numerics.LinearAlgebra.Vector<int>"]
Out:= NETType[MathNet.Numerics.LinearAlgebra.Vector`1[System.Int32],16]

However NETNew cannot create a vector object:

because there is no constructor with this type. The workaround is from taking a look at class list of the NETTypeInfo of the MathNet assembly:

NETInfo[assem, "Classes", "*Dense*"] is a call of such funciton with pattern match. I use this function when I notice that the C Sharp code in the online example calls the Dense.Build method to create a dynamic (a fancy way of using new) vector or matrix object. The dense method stores every item of the array. Contrary, the sparse method only store the non-zero entries.

The ....DenseVector type contains public constructors:

(Notice that NETTypeInfo can take the string name of the class/type/assembly as well)

To create a vector in the runtime, you just put a regular Mathematica vector of real numbers into the place of arguments:

In:= a = NETNew[ "MathNet.Numerics.LinearAlgebra.Double.DenseVector", {1, 2, 3, 4}] 
Out:= <<NETObject[MathNet.Numerics.LinearAlgebra.Double.DenseVector]>>

In:= b = NETNew[ "MathNet.Numerics.LinearAlgebra.Double.DenseVector", 10] 
Out:= <<NETObject[MathNet.Numerics.LinearAlgebra.Double.DenseVector]>>
(* b is {0,0,...,0} *)

In:= c = NETNew["MathNet.Numerics.LinearAlgebra.Double.DenseMatrix", 2, 2, {1,2,3,4}]
Out:= <<NETObject[MathNet.Numerics.LinearAlgebra.Double.DenseMatrix]>>
(* c is a col-major matrix: {{1,3},{2,4}}*)

To get the result back to Mathematica, use the method associated with these types:

 In:= a@ToArray[]
 Out= {1.,2.,3.,4.}

 In:= c@ToArray[]
 Out= {{1.,3.},{2.,4.}}

I can do this because the return type of the ToArray is double[] or double[,], which are basic System type in C sharp and Mathematica can convert these type to Real automatically. One more thing to say here is that Mathematica kernel is smart enough to avoid namespace/context clashing:

In:= res=(c@Transpose[])@Inverse[] (*MathNet's Transpose and Inverse*)
Out= « NETObject[MathNet.Numerics.LinearAlgebra.Double.DenseMatrix]»

Check the result:

In:= res@ToArray[]
Out= {{-2.,1.},{1.5,-0.5}}

which is the same as the familiar Mathematica implementation:

In:= Inverse[Transpose[c@ToArray[]]] (*the Mathematica Inverse and Transpose*)
Out= {{-2.,1.},{1.5,-0.5}}