Hello, everyone! I am using DSolve to solve a differential equation which is somewhat complicated. After several tens of minutes of waiting, I got a result, but with integration symbol.
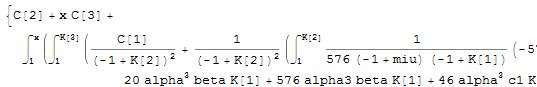
and with unknown K1, K2, K3 as follows. 
But when I use DSolve with simpler differential equations, I can get analytical result.

Will you please tell me how to get analytical result with my complicated eqation?
Thanks and best regards!
Jiujiang
(The software is a trial version V10.0.1.0, 64bit )