Those who are interested in step-by-step solution of linear equation systems might find the Student's Linear Equations section of my Presentations Application useful. It allows matrix structures to be composed in detail with row and column names and dividers, You can display any intermediate or final result in the notebook and there is also a side window that displays the current state of the matrix structure. The display elements can be used as paste buttons to paste the structure locations into the commands.
Duplicating Daniel's example would look like the following. The LEWhiteboard gives the window display and LEPrint gives the notebook display.
<< Presentations`
case1 = LECreate[4, 8];
LEWhiteboard[case1]
Then composing the matrix
LEInsertColumnNames[case1, 5, {R1, R2, R3, R4}]
LEColumnDividers[case1, {4}]
LEInsertMatrix[case1, {1, 1}, {{1, 7, 5, 0}, {5, 8, 6, 9}, {2, 1, 6, 4}, {8, 1, 2, 4}}]
LEInsertMatrix[case1, {1, 5}, IdentityMatrix[4]]
LEPrint[case1]
This gives:
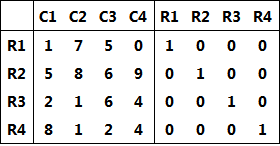
Then the standard Gaussian reduction can be done with:
LEMakeEchelonForm[case1, {1, 1}, {4, 4}]
LEPrint[case1]
which gives:
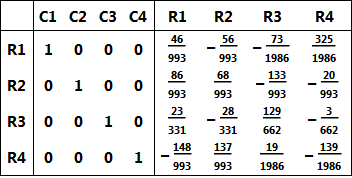
It's also possible to specify that only the below diagonal elements are to be zeroed. This example was fairly simple and I won't give other examples here but the system allows much more detail.
The commands for composing structures are: LECreate, LEInsertRowNames, LEInsertColumnNames, LEInsertMatrix, LERowDividers, LEColumnDividers, LEContravariant, LESetIOptions, LENumberFunction.
The commands for displaying the structures are: LEPrint and LEWhiteboard.
The commands for operating on structures are: LEScaleRow, LEAddToRow, LESumRows, LETargetValue, LESwapRows, LESwapColumns, LEPivot, LESimplexPivot, LEMakeExhelonForm, LEMaxFeasibleAddition, LEMakeInteger.
The commands for extracting from structures are: LEExtractRowNames, LEExtractColumnNames, LEExtractMatrix, LERowExpression, LEColumnExpressions, LEReactionEquation, LEChemicalFormula.
One novel feature in the commands is the facility for contravariant columns (covariant being the standard practice). Some columns can be covariant and some contravariant. Contravariant columns roughly correspond to packages of things so if you put more items in a package you need fewer of the packages.
This is mainly useful for didactic purposes and solving small systems, or maybe just for seeing what the heck is going on. One of the troubles with calculating with matrices is that they don't automatically carry context. Are you dealing with the matrix, or its inverse, or its transpose or its inverse transpose? Carrying row and column names adds context and helps to keep things straight.