The MRB constant ("C"MRB) = 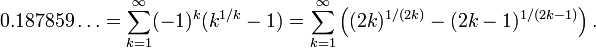
Here are three programs for calculating digits of "C"MRB.
Can you prove why they work?
Here is the first one:
1/2 - Pi/2 +
NSum[(-1)^n*(n^(1/n) - Pi), {n, 1, \[Infinity]},
Method -> "AlternatingSigns", WorkingPrecision -> 3000,
PrecisionGoal -> 3000]
Here is the second one:
eta[s_] := (1 - 2^(1 - s)) Zeta[s];
a[i_] := Derivative[i][eta][0];
c[j_] := Sum[Binomial[j, d]*(-1)^d*d^(j - d), {d, 1, j}];
-N[Sum[c[m]/m!*a[m], {m, 1, 40}], 6]
Here is one that is not so short:
(*Newer loop with Newton interior.*)prec = 1000;(*Number of required \
decimals.*)expM[pr_] := Module[{a, d, s, k, b, c}, n = Floor[1.32 pr];
Print["Iterations required: ", n];
d = N[(3 + Sqrt[8])^n, pr + 10];
d = Round[1/2 (d + 1/d)];
{b, c, s} = {-1, -d, 0};
T0 = SessionTime[];
Do[c = b - c;
x = N[E^(Log[k + 1]/(k + 1)), iprec = Ceiling[prec/128]];
pc = iprec;
Do[nprec = Min[2 pc, pr];
x = SetPrecision[x, nprec];(*Adjust precision*)
x = N[x - x/(k + 1) + 1/x^k, nprec];
pc *= 2;
If[nprec >= pr, Break[]], {ct, 1, 19}];
s += c*(x - 1);
b *= 2 (k + n) (k - n)/((k + 1) (2 k + 1));
If[Mod[k, 1000] == 0,
Print["Iterations: ", k, " Cumulative time (sec): ",
SessionTime[] - T0];], {k, 0, n - 1}];
N[-s/d, pr]];
t2 = Timing[MRBtest2 = expM[prec];]
If you can come up with others, please post them!
I think the last two are related, somehow.
Here is some help on proving why the first one works: (See attached notebook.)
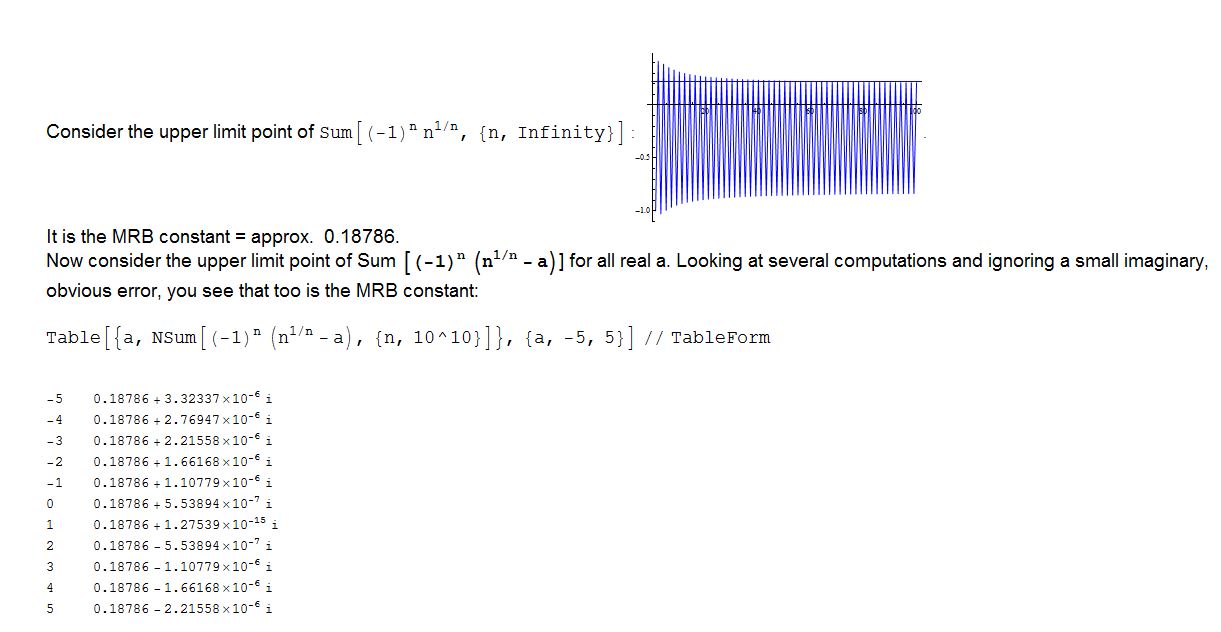
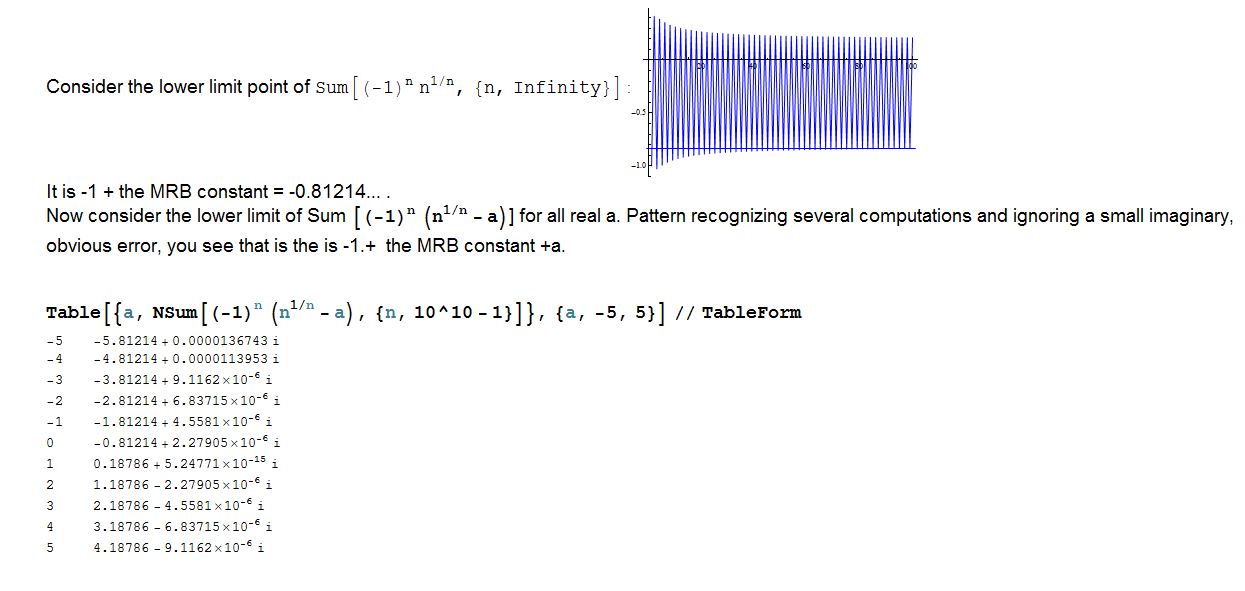
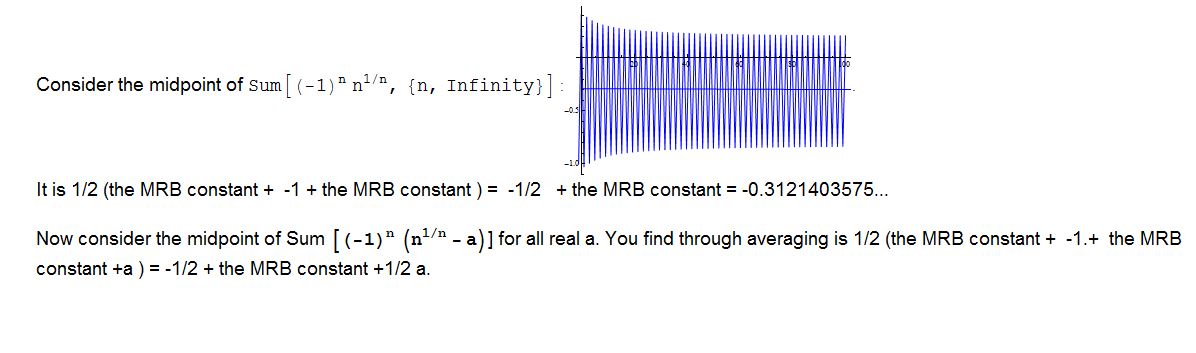
 Attachments:
Attachments: