Message Boards Message Boards

0
|
4539 Views
|
2 Replies
|
0 Total Likes
View groups...
Share
Share this post:

Why Programs give the MRB constant?

The MRB constant ("C"MRB) = 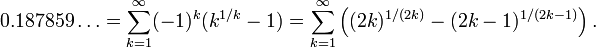enter image description here

Here are three programs for calculating digits of "C"MRB.

Can you prove why they work?

Here is the first one:

1/2 - Pi/2 + 
 NSum[(-1)^n*(n^(1/n) - Pi), {n, 1, \[Infinity]}, 
  Method -> "AlternatingSigns", WorkingPrecision -> 3000, 
  PrecisionGoal -> 3000]

Here is the second one:

eta[s_] := (1 - 2^(1 - s)) Zeta[s];
a[i_] := Derivative[i][eta][0];
c[j_] := Sum[Binomial[j, d]*(-1)^d*d^(j - d), {d, 1, j}];
-N[Sum[c[m]/m!*a[m], {m, 1, 40}], 6]

Here is one that is not so short:

(*Newer loop with Newton interior.*)prec = 1000;(*Number of required \
decimals.*)expM[pr_] := Module[{a, d, s, k, b, c}, n = Floor[1.32 pr];
  Print["Iterations required: ", n];
  d = N[(3 + Sqrt[8])^n, pr + 10];
  d = Round[1/2 (d + 1/d)];
  {b, c, s} = {-1, -d, 0};
  T0 = SessionTime[];
  Do[c = b - c;
   x = N[E^(Log[k + 1]/(k + 1)), iprec = Ceiling[prec/128]];
   pc = iprec;
   Do[nprec = Min[2 pc, pr];
    x = SetPrecision[x, nprec];(*Adjust precision*)
    x = N[x - x/(k + 1) + 1/x^k, nprec];
    pc *= 2;
    If[nprec >= pr, Break[]], {ct, 1, 19}];
   s += c*(x - 1);
   b *= 2 (k + n) (k - n)/((k + 1) (2 k + 1));
   If[Mod[k, 1000] == 0, 
    Print["Iterations: ", k, "    Cumulative time (sec): ", 
      SessionTime[] - T0];], {k, 0, n - 1}];
  N[-s/d, pr]];

t2 = Timing[MRBtest2 = expM[prec];]

If you can come up with others, please post them!

I think the last two are related, somehow.

Here is some help on proving why the first one works: (See attached notebook.)

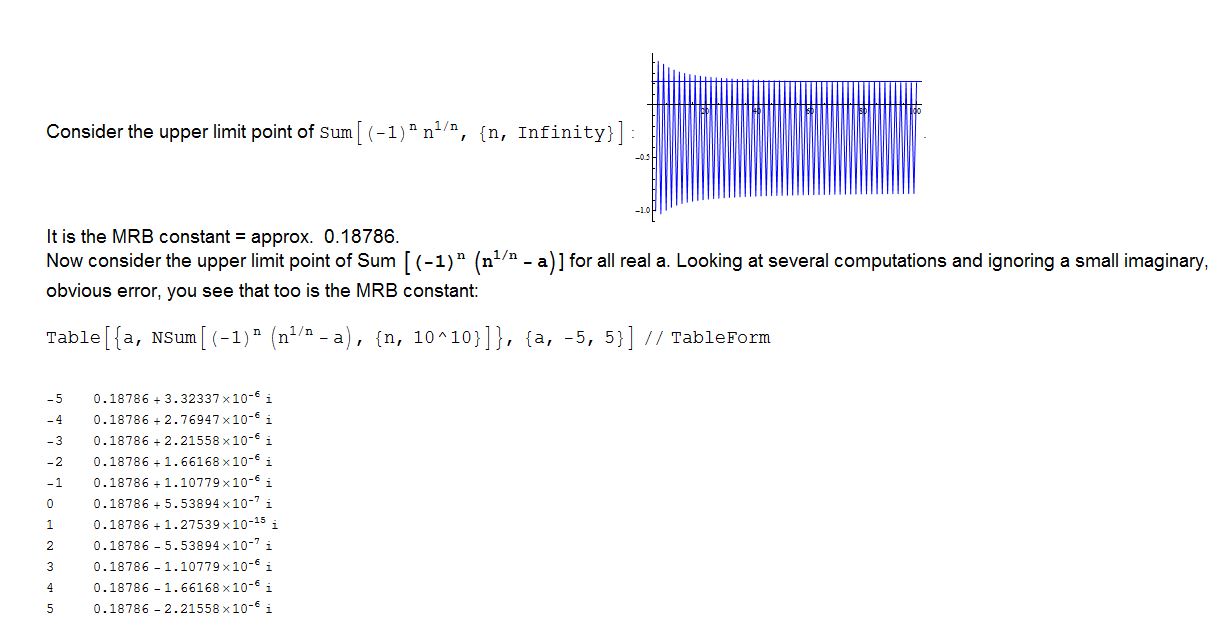
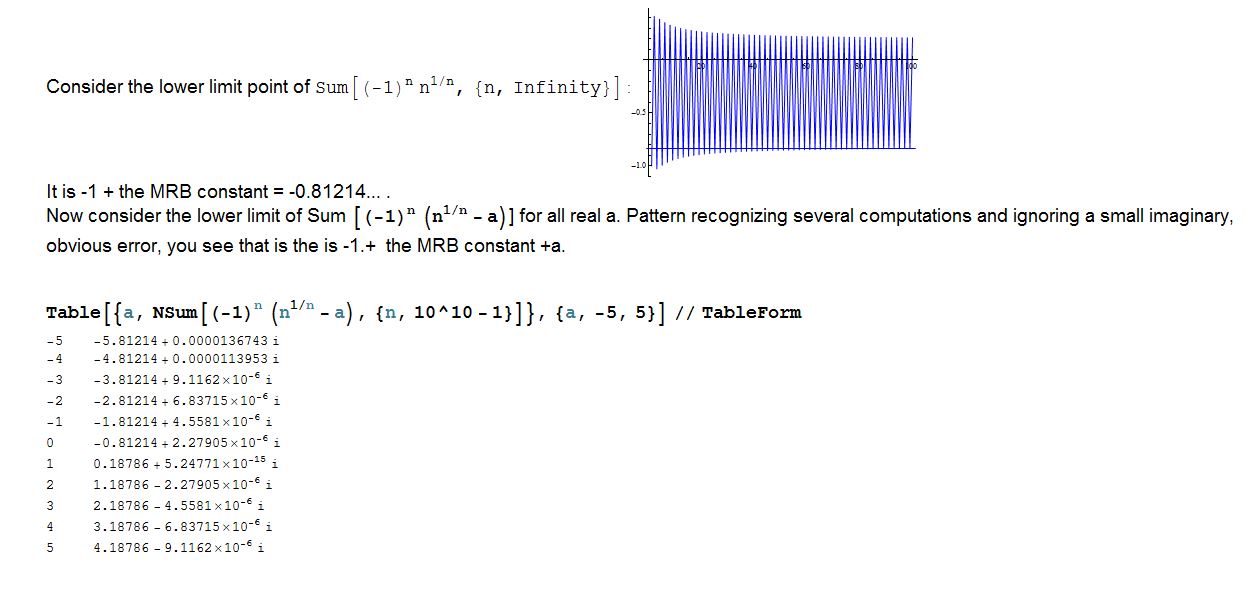
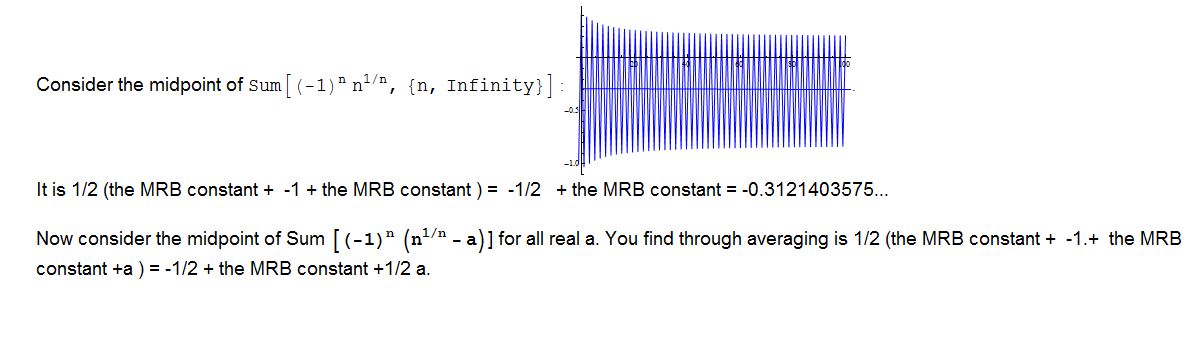
enter image description here enter image description here enter image description here

Attachments:
POSTED BY: Marvin Ray Burns
2 Replies
Sort By:

I wouldn't say that first actually "works". It depends on vagaries of NSum implementation, I think. What happens, as in the graphs posted, is that the odd partial sums and even partial sums average to the constant. The sum of Pi terms in such pairs is simply pi (these cancel in the even sums, and cancel with one +pi left over in the odd partial sums). So the contribution of Pi's in the averaged sum below is zero (from -Pi/2-Pi/2+Pi).

((1/2 - Pi/2 + 
     NSum[(-1)^n*(n^(1/n) - Pi), {n, 1, 2000}, 
      NSumTerms -> 2000]) + (1/2 - Pi/2 + 
     NSum[(-1)^n*(n^(1/n) - Pi), {n, 1, 2001}, NSumTerms -> 2001]))/2

If you add those 1/2 terms above you realize that the result, +1, is exactly what would survive had there been 1's in place of the pi's in the two summations. But, had that been the case, we'd be working with the MRB constant by definition.

Upshot: Method 1 only works if there is an averaging done. Which might make it numerically a good method, I don't know.
POSTED BY: Daniel Lichtblau

A discussion by Henri Cohen, Fernando Rodriguez Villegas, and Don Zagier of the algorithm used in program three for acceleration is found here.

In specific, it is the following: enter image description here

In Program 2, a Crandall algorithm is being used which is the following, where B is the MRB constant and eta is the Dirichlet eta function:

enter image description here
POSTED BY: Marvin Ray Burns
Reply to this discussion
Community posts can be styled and formatted using the Markdown syntax.
Tag limit exceeded
Note: Only the first five people you tag will receive an email notification; the other tagged names will appear as links to their profiles.
Reply Preview
Attachments
Remove
or Discard

Group Abstract Group Abstract