Suba,

Thanks for the clarification. I think you should add an example of making an open loop pole zero plot to the RootLocusPlot documentation because there are a few subtle options that need to be set and explained:

1. PoleZeroMarkers option takes a list of the {open-loop poles, closed-loop poles, open-loop zeros} and by putting "" for the closed loop poles, it no longer draws any closed loop poles.
2. The value for k must be small so that the root locus that is drawn is not visible on the plot. In the example above, k=1 is small compared to the pole/zero values.

But in this documentation example, it would leave colored loci lines on the plot:

RootLocusPlot[
 TransferFunctionModel[{{(k (10 + s^2))/(20 - 4 s + s^4)}}, s, 
  SamplingPeriod -> None, SystemsModelLabels -> None], {k, 0, 1}, 
 PoleZeroMarkers -> {Style["\[Times]", 30], "", 
   Style["\[SmallCircle]", 40]}, PlotRange -> {{-2, 2}, {-6, 6}}]

Which can be removed with setting a tiny value for k:

RootLocusPlot[
 TransferFunctionModel[{{(k (10 + s^2))/(20 - 4 s + s^4)}}, s, 
  SamplingPeriod -> None, SystemsModelLabels -> None], {k, 0, 0.0001}, 
 PoleZeroMarkers -> {Style["\[Times]", 30], "", 
   Style["\[SmallCircle]", 40]}, PlotRange -> {{-2, 2}, {-6, 6}}]

To get:

Regards,

Neil

Neil: The way to get RootLocusPlot to plot a pole-zero plot is the following.

RootLocusPlot[ k tfm3[s], {k, 0, 1}, 
 PoleZeroMarkers -> {Style["\[Times]", 30], "", 
   Style["\[SmallCircle]", 40]}, PlotStyle -> None, 
 PlotRange -> {Automatic, {-1000, 1000}}, AxesOrigin -> {0, 0}]

Koushik: The following should have worked, but it does not. This will directly change the size of the default markers. I will commit a fix for this.

Control`PoleZeroPlot[tfm3, 
 PoleZeroMarkers -> {{Automatic, 20}, {Automatic, 20}}, 
 PlotRange -> {Automatic, {-1000, 1000}}, AxesOrigin -> {0, 0}]

For now, the workaround is what Neil mentioned.

Control`PoleZeroPlot[tfm3, 
 PoleZeroMarkers -> {Style["\[Times]", 30], 
   Style["\[SmallCircle]", 40]}, 
 PlotRange -> {Automatic, {-1000, 1000}}, AxesOrigin -> {0, 0}]

Please format your code with the code sample button on the toolbar -- it makes it easier to read and to copy and paste.

You need to use PoleZeroPlot with options -- you can't use inline notation (@). Using the code button :) it looks like this:

Control`PoleZeroPlot[tfm3, 
 PoleZeroMarkers -> {Style["\[Times]", 30], 
   Style["\[SmallCircle]", 40], Automatic}, 
 PlotRange -> {Automatic, {-500, 500}}, AxesOrigin -> {0, 0}]

You should play with the style values to get something that looks ok. This is a hard thing to plot because you have a zero and a pole in the same place so the plot does not look great.

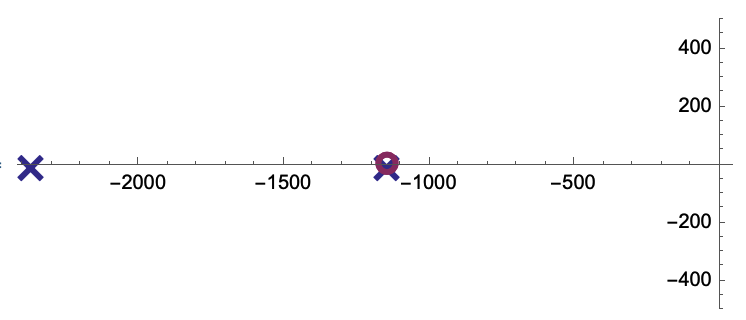
Normally, I would suggest that you do not use the unsupported/undocumented function and use RootLocusPlot instead:

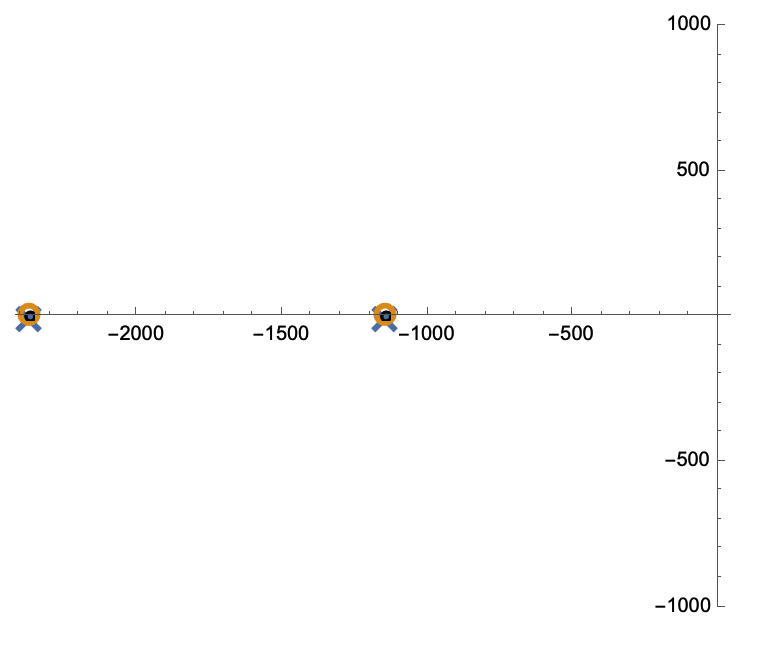
RootLocusPlot[tfm3, {k, 0, 1}, FeedbackType -> None, 
 PoleZeroMarkers -> {Style["\[Times]", 30], 
   Style["\[SmallCircle]", 40], Automatic}, 
 PlotRange -> {Automatic, {-1000, 1000}}, AxesOrigin -> {0, 0}]

However, for some reason, it adds an extra zero on the plot. Maybe @Suba Thomas can explain what is happening here (Is it a bug??). if not, Suba, you should add an option to RootLocusPlot to just plot the open loop poles and an extra documentation example should be added to show how to make an open loop pole zero plot.

Lastly, another way to get publication quality plots exactly how you want them is to use TransferFunctionPoles and TransferFunctionZeros to get the poles and zeros and plot them using ListPlot and set various options to get exactly what you want (although this involves more effort in setting every option).

Regards,

Neil

You can use the same options as RootLocusPlot:

PoleZeroMarkers -> {Style["T", Large, Background -> Pink]}

Regards

You can also use Control`PoleZeroPlot.

Control`PoleZeroPlot@ButterworthFilterModel[12]

This is an undocumented function, but it's very straightforward. Given a TransferFunctionModel tfm, its pole zero plot can be obtained as

Control`PoleZeroPlot[tfm]

You are probably confused with the prefix operator @.

Control`PoleZeroPlot@tfm

also gives the same result.