"The Turkana Basin Institute and the National Museums of Kenya teamed up with a software firm to create africanfossils.org to showcase many of the iconic fossils discovered in East Africa. Files to print 3-D copies for educational purposes can be downloaded from the site." National Geographic reports. You can 3D print a replica of a million year old skull for your own collection. Rotatable models are viewable online:

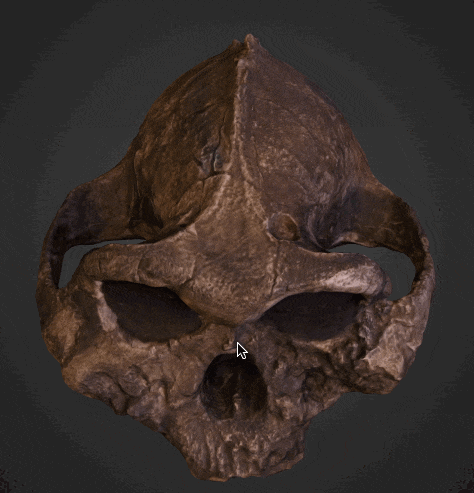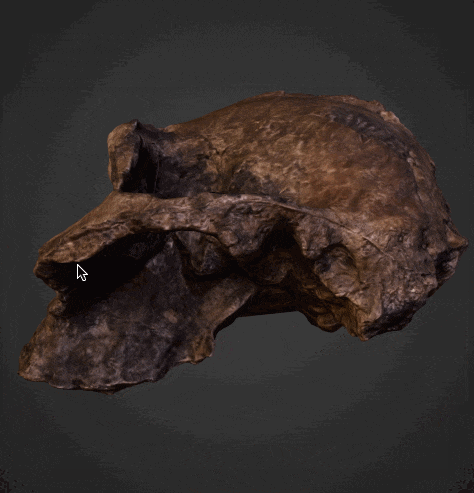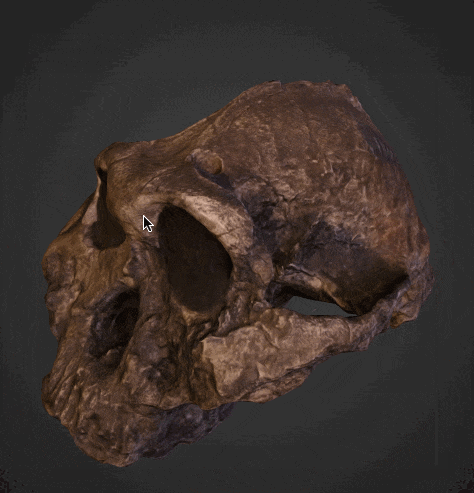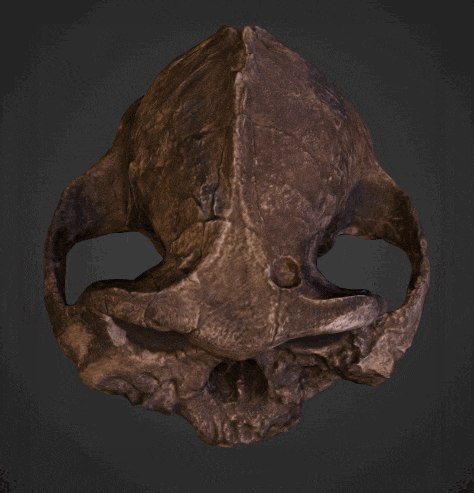
With the Wolfram Language you can not only view the relics, but also compare them visually and even numerically. Let's import the models of Paranthropus Boisei and Homo Erectus from the museum's website:

{skullV1, skullP1} = Import["http://wolfr.am/1QKeqSOX", {"STL", #}] & /@ {"VertexData", "PolygonData"};
{skullV2, skullP2} = Import["http://wolfr.am/1QKG9c8D", {"STL", #}] & /@ {"VertexData", "PolygonData"};

The skulls are significantly different in size and to compare the shape it would make sense to rescale the data:

Manipulate[Graphics3D[{
 GraphicsComplex[Rescale[skullV1], {EdgeForm[], FaceForm[Directive[Opacity[op1], Orange]], Polygon[skullP1 // First]}],
 GraphicsComplex[Rescale[skullV2], {EdgeForm[], FaceForm[Directive[Opacity[op2], Blue]], Polygon[skullP2 // First]}]}, 
 ViewPoint -> Top, SphericalRegion -> True, Boxed -> False]
 , {{op1, .5}, 0, 1}
 , {{op2, .5}, 0, 1}]

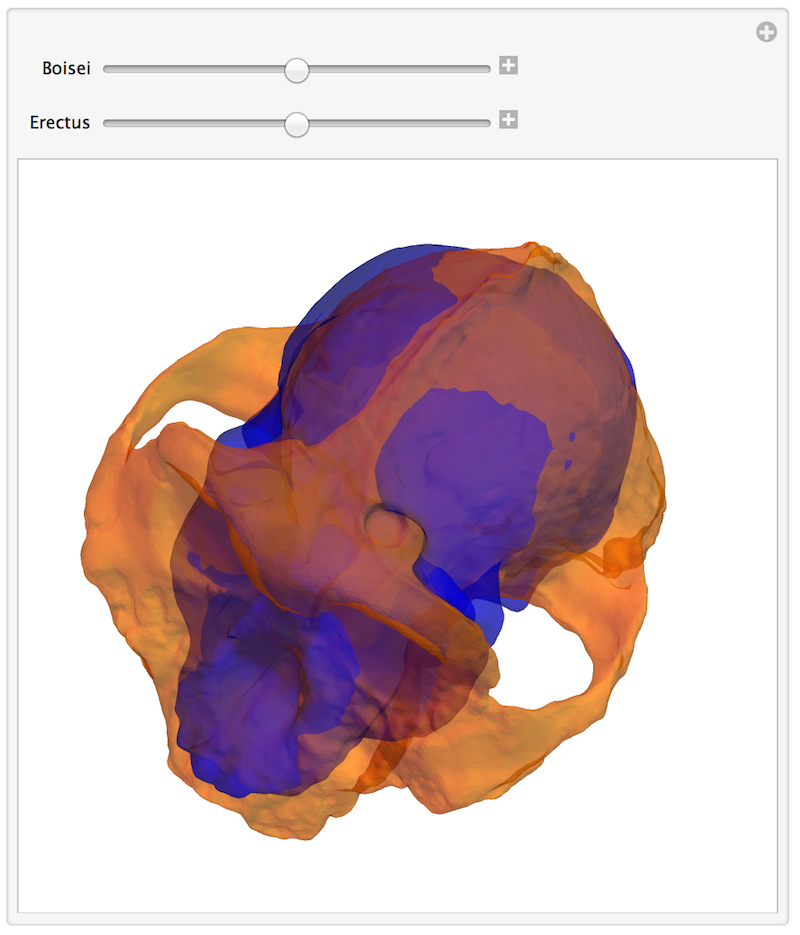
We also can compare numerically. Original measured sizes reported by museums are:

Paranthropus Boisei: x=185.50; y=177.70; z=139.30 mm Homo Erectus: x=179.73; y=175.15; z=275.15 mm

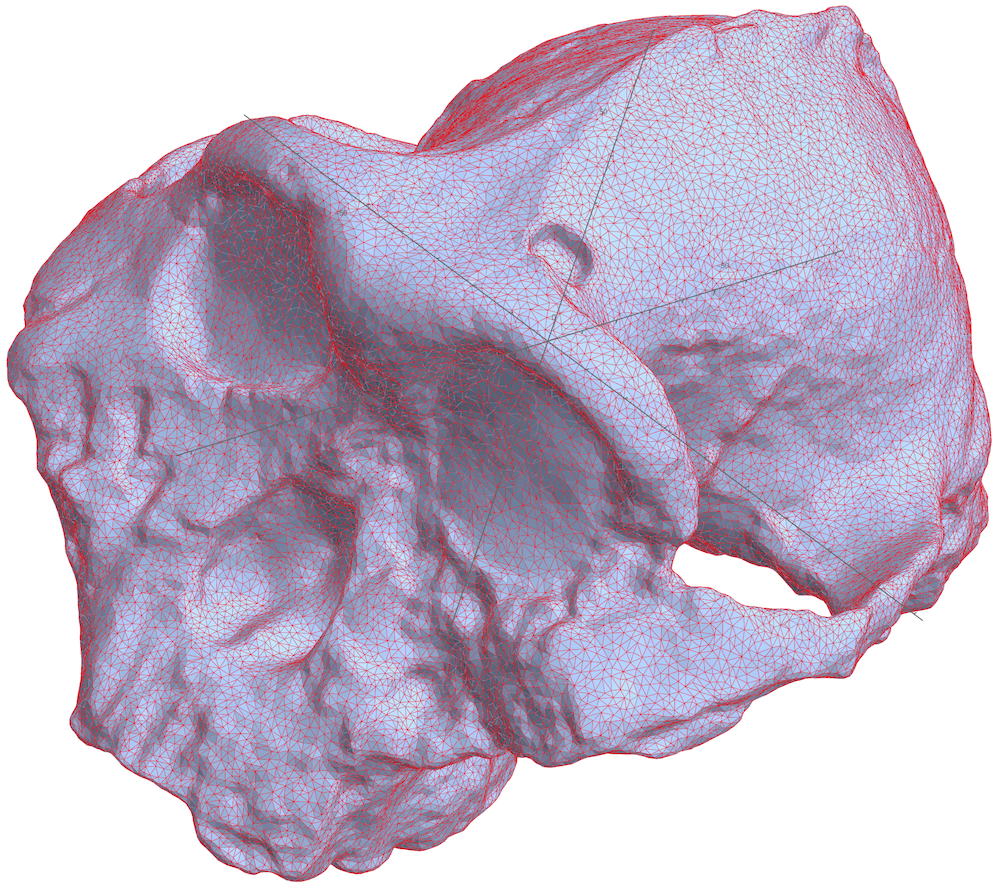
We can use our computational geometry functionality to compute the volumes, but first lets check that models are indeed to scale (watch units on axes):

Show[MeshRegion[skullV1, Polygon[skullP1 // First]], 
    Axes -> True, PlotRangePadding -> 0, AxesOrigin -> {0, 0, 0}, SphericalRegion -> True]

Now, both skulls are missing jaws, so the comparison is fair while of course is very approximate. Still we see that Homo Erectus has ~3 times larger skull by volume which is given in cubic millimeters.

Volume[BoundaryMeshRegion[skullV1, Polygon[skullP1 // First]]]
Out[]= 1.13324*10^6

Volume[BoundaryMeshRegion[skullV2, Polygon[skullP2 // First]]]
Out[]= 3.44515*10^6