Thank you S M Blinder. Ok now I can solve the equation, but when i plot the result, it is totally different from which I obtain with NDSolveValue. What do you think about? Thank you
Clear["Global`*"];
Needs["DifferentialEquations`InterpolatingFunctionAnatomy`"];
LaplaceEquation2D = {D[u[x, y], {x, 2}] + D[u[x, y], {y, 2}] == 0}
Xm = DSolve[{D[X[x], {x, 2}]/X[x] == 1, X[0] == 0, X[20] == 1}, X[x],
x]
Ym = DSolve[{D[Y[y], {y, 2}]/Y[y] == -1, Y[0] == 0, Y[20] == 2}, Y[y],
y]
u[x, y] = (X[x] /. Xm)*(Y[y] /. Ym);
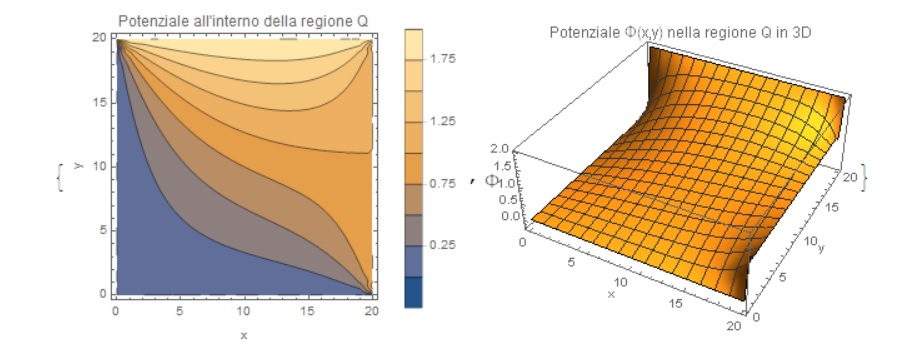
{ContourPlot[Evaluate[u[x, y]], {x, 0, 20}, {y, 0, 20},
FrameLabel -> {"x", "y"},
PlotLabel -> "Potenziale all'interno della regione Q",
ImageSize -> 250,
PlotLegends -> Automatic],
Plot3D[Evaluate[u[x, y]] , {x, 0, 20}, {y, 0, 20}, ImageSize -> 300,
AxesLabel -> {"x", "y", Style["\[CapitalPhi]", 15]},
PlotLabel ->
Style["Potenziale \[CapitalPhi](x,y) nella regione Q in 3D", 12]]}
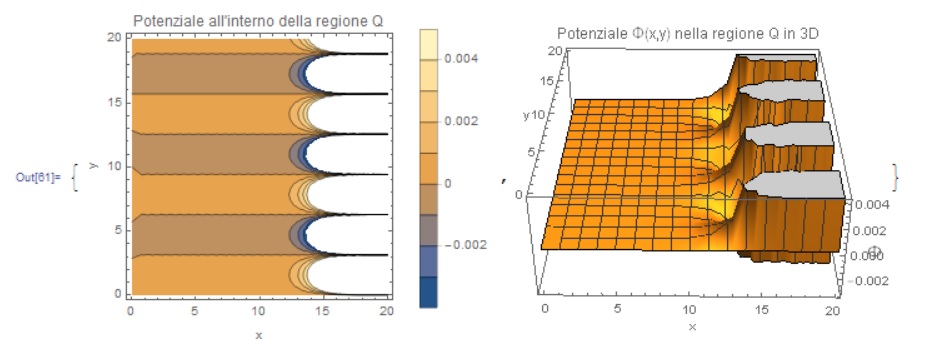
uval = NDSolveValue[{D[u[x, y], {x, 2}] + D[u[x, y], {y, 2}] == 0,
u[x, 0] == 0, u[x, 20] == 2, u[0, y] == 0, u[20, y] == 1},
u, {x, 0, 20}, {y, 0, 20}]
{ContourPlot[uval[x, y], {x, 0, 20}, {y, 0, 20},
FrameLabel -> {"x", "y"},
PlotLabel -> "Potenziale all'interno della regione Q",
ImageSize -> 250,
PlotLegends -> Automatic],
Plot3D[uval[x, y] , {x, 0, 20}, {y, 0, 20}, ImageSize -> 300,
AxesLabel -> {"x", "y", Style["\[CapitalPhi]", 15]},
PlotLabel ->
Style["Potenziale \[CapitalPhi](x,y) nella regione Q in 3D", 12]]}