Looks like something is missing from the Limit function:

Limit[Sin[Sqrt[x^2 - 1]] - Sin[Sqrt[x^2 + 1]], x -> x0]

where x0 is set to the desired value. The function in question also has multiple values of x0 that result in a limit/value of zero (although it doesn't appear that it's necessary to use Limit - but I must be missing something).

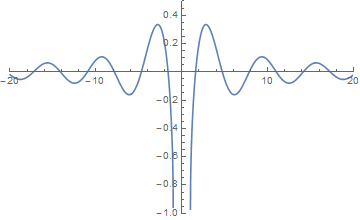
Plot[Sin[Sqrt[x^2 - 1]] - Sin[Sqrt[x^2 + 1]], {x, -20, 20}, 
 PlotRange -> {{-20, 20}, {-1, 0.5}}]

results in

Sorry! I have omitted the limit point: Limit[Sin[Sqrt[x^2 - 1]] - Sin[Sqrt[x^2 + 1]], x -> Infinity]. By using the command Plot[Sin[Sqrt[x^2 - 1]] - Sin[Sqrt[x^2 + 1]], {x, 0, 100}, PlotRange -> All] we can see the limit is equal to 0; but Mathematica 9 gives Interval[{-2,2}]!

Uh, this isn't the kind of answer I like to get but for Mathematica 10.0.1 (Windows 7 and a more recent version than 8 and 9 that you mention), I get the correct answer:

In[1]:= Limit[Sin[Sqrt[x^2 - 1]] - Sin[Sqrt[x^2 + 1]], x -> Infinity]

Out[1]= 0

And for whatever it's worth I get the same response as you for version 9.