Hey there, community!
I have recently been working with the new FEM-package included in Mathematica 10. I have a 2D mesh and two interpolating functions (call them uif and vif) obtained by solving a differential equation in the mesh using NDSolve. The mesh is similar to the one shown below, only denser. My problem now is that, given values u0 and v0, I need to find the point where uif[x,y] = u0 and vif[x,y] = v0.
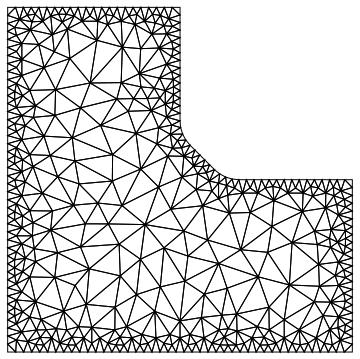
Now, since uif and vif are defined on the mesh, I would naturally want to do something like this:
NMinimize[{Norm[{u0 - uif[x, y], v0 - vif[x, y]}], {x, y} \[Element] mesh}, {x, y}]];
Here "{x,y} [Element] mesh" indicates that the point (x,y) lies inside the mesh. Unfortunately, the above code results in the following error:
NMinimize::elemc: "Unable to resolve the domain or region membership condition {x,y} \[Element] <<1>>.
So, is there a way to convert the mesh into a region that I can pass on to NMinimize? Previously I tried defining the region explicitly using unions and differences of disks and rectangles, or implicitly using equations for $x$ and $y$, but due to a number of bugs (or restrictions) with the regions and with the FEM package, this is unfortunately not an option.
The mesh is simply-connected and I do have direct access to the boundary mesh if necessary.
-Jonatan