Difference in behavior between RegionNearest for a polygon's centroid in 2D vs 3D
Consider a simple 2-d polygon whose centroid is outside of the polygon:
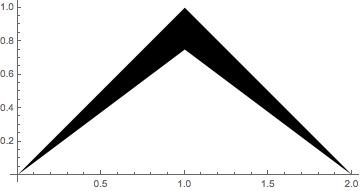
Here is the polygon:
region = Polygon[{{0, 0}, {1, 1}, {2, 0}, {1, 3/4}}];
Graphics[region, Axes -> True]
giving
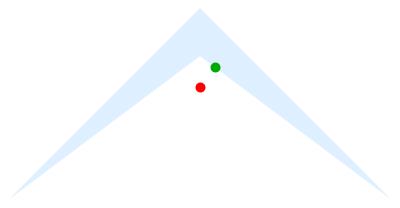
Now plot the centroid along with the point in the region closest to the centroid (yes there are technically two that are closest =because of teh symmetry, but RegionNearest chooses one--that's fine):
Graphics[{AbsolutePointSize[10], LightBlue, region, Red,
Point[RegionCentroid[region]], Darker@Green,
Point[RegionNearest[region, RegionCentroid[region]]]},
ImageSize -> 400]
giving (red point for the centroid and green point for the nearest in the region):
Now let's do this in 3D:
region3d = Polygon[{{0, 0, 0}, {1, 1, 0}, {2, 0, 0}, {1, 3/4, 0}}];
Graphics3D[region3d, Axes -> True]
giving
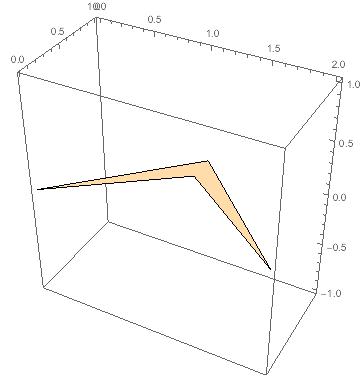
and
Graphics3D[{AbsolutePointSize[10], LightBlue, region3d, Red,
Point[RegionCentroid[region3d]], Darker@Green,
Point[RegionNearest[region3d, RegionCentroid[region3d]]]},
ImageSize -> 400]
giving
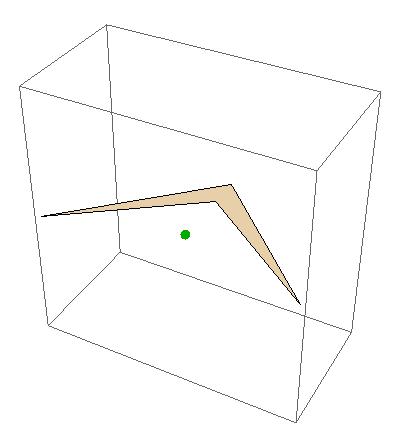
So the obvious question here is why the nearest point to the centroid is now at the centroid.