Difference in behavior between RegionNearest for a polygon's centroid in 2D vs 3D

Consider a simple 2-d polygon whose centroid is outside of the polygon:

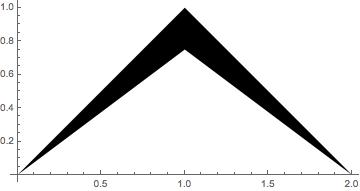
Here is the polygon:

region = Polygon[{{0, 0}, {1, 1}, {2, 0}, {1, 3/4}}];
Graphics[region, Axes -> True]

giving

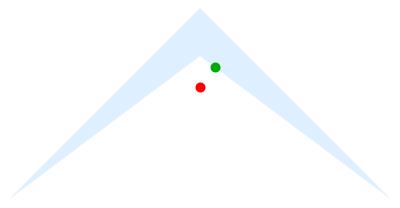
Now plot the centroid along with the point in the region closest to the centroid (yes there are technically two that are closest =because of teh symmetry, but RegionNearest chooses one--that's fine):

Graphics[{AbsolutePointSize[10], LightBlue, region, Red, 
  Point[RegionCentroid[region]], Darker@Green, 
  Point[RegionNearest[region, RegionCentroid[region]]]}, 
 ImageSize -> 400]

giving (red point for the centroid and green point for the nearest in the region):

Now let's do this in 3D:

region3d = Polygon[{{0, 0, 0}, {1, 1, 0}, {2, 0, 0}, {1, 3/4, 0}}];
Graphics3D[region3d, Axes -> True]

giving

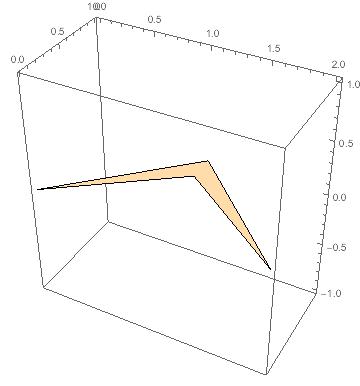
and

Graphics3D[{AbsolutePointSize[10], LightBlue, region3d, Red, 
  Point[RegionCentroid[region3d]], Darker@Green, 
  Point[RegionNearest[region3d, RegionCentroid[region3d]]]}, 
 ImageSize -> 400]

giving

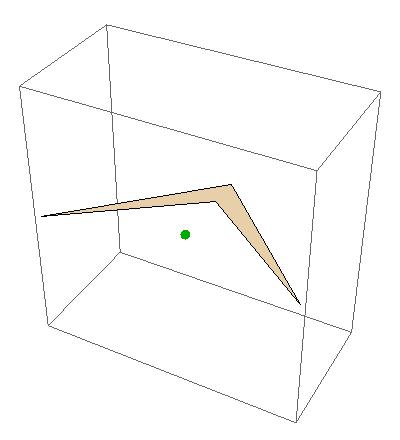
So the obvious question here is why the nearest point to the centroid is now at the centroid.