skinks = {56, 19, 28, 18, 24, 14, 9}; kskinks = 7;

myBBBlik[data_, kdata_, f0_?NumericQ, p_?NumericQ, w_?NumericQ, alpha_?NumericQ, beta_?NumericQ] :=

    Block[
    {K, fj, pj, loglik},
    K = kdata;
    fj = Prepend[PadRight[data, K], f0];
    pj = Table[
        PDF[MixtureDistribution[{w, 1 - w}, {BinomialDistribution[K, p], 
        BetaBinomialDistribution[alpha, beta, K]}], j],
        {j, 0, K}
    ];
    loglik = LogGamma[Tr[fj] + 1] - Tr[LogGamma[fj + 1]] + Tr[fj*Log[pj]];
    Print[loglik];
    loglik
];

pars = {f0,p,w,allpha,beta};
cons = {f0 > 0 && 0 < p < 1 && 0 < w < 1 && alpha > 0 && beta > 0};
cons2 = {f0 > 0 , 0 < p < 1 , 0 < w < 1 , alpha > 0 , beta > 0};

NMaximize[{myBBBlik[skinks, kskinks, Sequence @@ pars], cons}, pars, Method -> {"RandomSearch", "SearchPoints" -> Automatic}]

Note that it may crash your kernel!

If you take out the line Print[loglik];, it will give your the correct answer. Works perfect. However, if you leave it in and it may crash your kernel, but you will see something (unbelievable && unexpected) like this: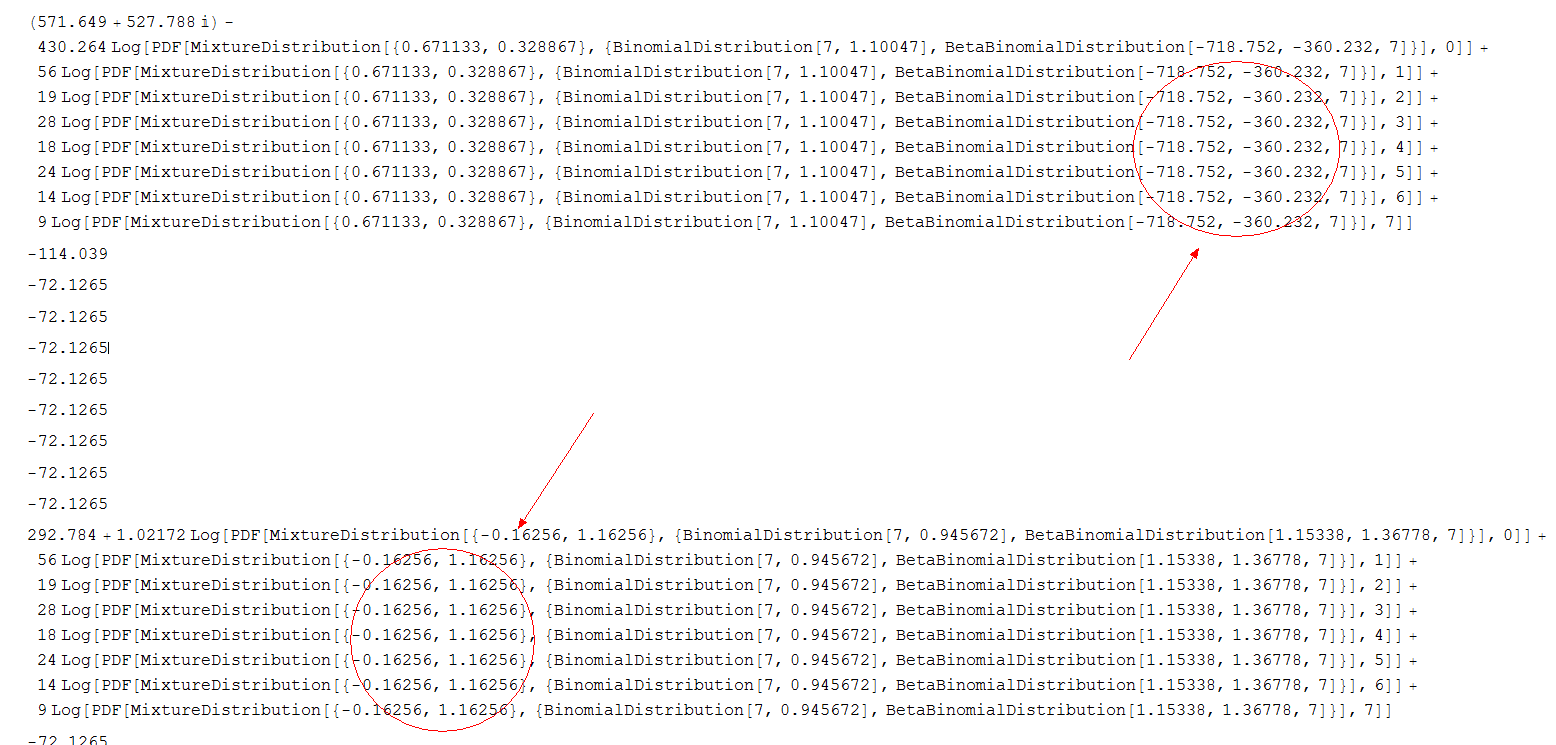

Why does it even call the function myBBBlik? Values like -717.752 and -360.232 are long way from 0. These would not considered when you have alpha>0,beta>0. This is just really something I don't understand the way MMA works.

I am using MMA 10.0.2 X64 (win)