Perhaps, this will help.
DSolve[y''[x] + 4 y'[x] + 8 y[x] == x 3 x Cos[x], y, x]
Now, the solution is a bit large. As you did not provide any boundary condition, I choose the integration constants to be 1.
StreamPlot[{x,E^(-2 x) Cos[2 x] + E^(-2 x) Sin[2 x] +1/10985003 (48334 Cos[x] Cos[2 x] - 87880 x Cos[x] Cos[2 x] +54925 x^2 Cos[x] Cos[2 x] + 2250 Cos[2 x] Cos[3 x] -39000 x Cos[2 x] Cos[3 x] + 63375 x^2 Cos[2 x] Cos[3 x] -8788 Cos[2 x] Sin[x] + 65910 x Cos[2 x] Sin[x] -109850 x^2 Cos[2 x] Sin[x] + 8788 Cos[x] Sin[2 x] -65910 x Cos[x] Sin[2 x] + 109850 x^2 Cos[x] Sin[2 x] -11500 Cos[3 x] Sin[2 x] + 16250 x Cos[3 x] Sin[2 x] +42250 x^2 Cos[3 x] Sin[2 x] + 48334 Sin[x] Sin[2 x] -87880 x Sin[x] Sin[2 x] + 54925 x^2 Sin[x] Sin[2 x] +11500 Cos[2 x] Sin[3 x] - 16250 x Cos[2 x] Sin[3 x] -42250 x^2 Cos[2 x] Sin[3 x] + 2250 Sin[2 x] Sin[3 x] -39000 x Sin[2 x] Sin[3 x] + 63375 x^2 Sin[2 x] Sin[3 x])}, {x, 0, 10}, {y, -30, 10}]
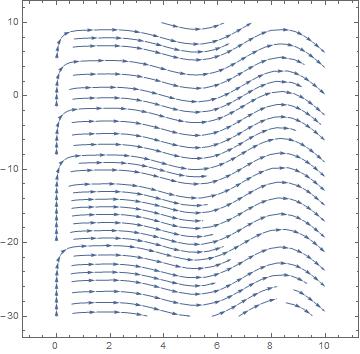
The plot is
Plot[y, {x, 0, 200}]
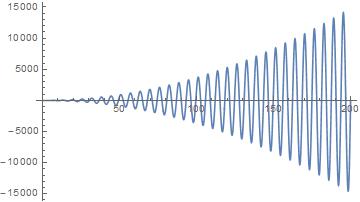
Sincerely, Suvadip