I spoke too soon. It does have a symbolic integral. The integral as given does not differ significantly from the one below, in which I changed the lower limits to zero. (Note: it is best to not begin user symbol names with capitals, since they might then conflict with reserved words. )
int0 = Integrate[
Exp[-(2 \[Pi] S Abs[x - y])/B]*Cos[(2 \[Pi] S)*(x - y)]*
Sin[1 \[Pi] x] Sin[1 \[Pi] y], {x, 0, 1}, {y, 0, 1}]
(*
(2 \[ExponentialE]^(-((2 \[Pi] S)/B)) (B^8 \[ExponentialE]^((2 \[Pi] \
S)/B)+B^7 \[ExponentialE]^((2 \[Pi] S)/B) \[Pi] S+8 B^6 \
\[ExponentialE]^((2 \[Pi] S)/B) S^2-8 B^8 \[ExponentialE]^((2 \[Pi] \
S)/B) S^2+12 B^5 \[ExponentialE]^((2 \[Pi] S)/B) \[Pi] S^3-4 B^7 \
\[ExponentialE]^((2 \[Pi] S)/B) \[Pi] S^3+16 B^4 \[ExponentialE]^((2 \
\[Pi] S)/B) S^4-96 B^6 \[ExponentialE]^((2 \[Pi] S)/B) S^4+16 B^8 \
\[ExponentialE]^((2 \[Pi] S)/B) S^4+48 B^3 \[ExponentialE]^((2 \[Pi] \
S)/B) \[Pi] S^5+32 B^5 \[ExponentialE]^((2 \[Pi] S)/B) \[Pi] S^5-16 \
B^7 \[ExponentialE]^((2 \[Pi] S)/B) \[Pi] S^5+64 B \
\[ExponentialE]^((2 \[Pi] S)/B) \[Pi] S^7+192 B^3 \[ExponentialE]^((2 \
\[Pi] S)/B) \[Pi] S^7+192 B^5 \[ExponentialE]^((2 \[Pi] S)/B) \[Pi] \
S^7+64 B^7 \[ExponentialE]^((2 \[Pi] S)/B) \[Pi] S^7+B^8 Cos[2 \[Pi] \
S]+8 B^6 S^2 Cos[2 \[Pi] S]-8 B^8 S^2 Cos[2 \[Pi] S]+16 B^4 S^4 Cos[2 \
\[Pi] S]-96 B^6 S^4 Cos[2 \[Pi] S]+16 B^8 S^4 Cos[2 \[Pi] S]-16 B^7 \
S^2 Sin[2 \[Pi] S]-64 B^5 S^4 Sin[2 \[Pi] S]+64 B^7 S^4 Sin[2 \[Pi] \
S]))/(\[Pi]^2 (B^2-4 B^2 S+4 S^2+4 B^2 S^2)^2 (B^2+4 B^2 S+4 S^2+4 \
B^2 S^2)^2)
*)
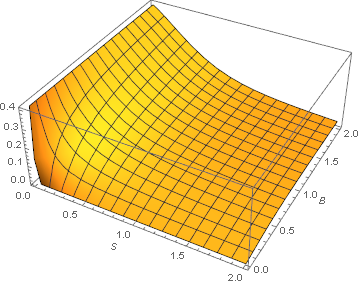
Plot3D[int0, {S, 0, 2}, {B, 0, 2}, AxesLabel -> {"S", "B"}]