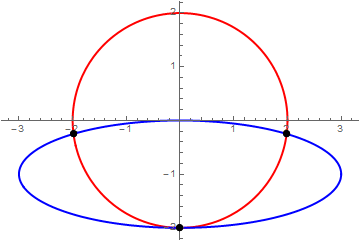
Since we want the intersection of the curves, we do not require t to be the same for each at the intersections. And the equality is really 2 equations, in x and y, so we need 2 independent variables. (Although Reduce or FindInstance would find the point where intersection occurs at t1 = t2.)
r1[t_] = {2 Cos[t], 2 Sin[t]};
r2[t_] = {3 Cos[t], Sin[t] - 1};
(* there are 2 independent variables *)
(* C[_]\[Rule]0 chhoses the principal solutions *)
sol = Solve[r1[t1] == r2[t2] // Evaluate, {t1, t2}] /. C[_] -> 0
(* {{t1\[Rule]-(\[Pi]/2),t2\[Rule]-(\[Pi]/2)},{t1\[Rule]-ArcTan[1/(3 \
Sqrt[7])],t2\[Rule]ArcTan[3/Sqrt[7]]},{t1\[Rule]-\[Pi]+ArcTan[1/(3 \
Sqrt[7])],t2\[Rule]\[Pi]-ArcTan[3/Sqrt[7]]}} *)
(* solution points *)
points = Point /@ {r1[t1], r2[t2]} /. sol // Flatten;
(* plot with solutions *)
parplot2 =
ParametricPlot[{r1[t], r2[t]}, {t, 0, 2 \[Pi]},
PlotStyle -> {{Red, Thick}, {Blue, Thick}},
Epilog -> {PointSize[.02], points}]