I made a few corrections. (One correction is the need to have separate variables for the parameters to generate the data and the parameters to be estimated.) For this log likelihood, Maximize works better than NSolve (in part I think because maximum likelihood estimator of mu is so close to the minimum data value). I also added some QA checks to see if the solution makes sense (which for just about any iterative method is highly recommended).
The estimate of the covariance matrix is also included but I wonder if because you are doing simulations and looking to characterize the sampling distributions of the maximum likelihood estimates, do you really need that? The "true" covariance matrix would be estimated from the results of the multiple simulations performed (unless you're also interested in the sampling properties of the estimated covariance matrix).
Below is the code:
(*Maximum likelihood example*)
(*Set parameter values*)
n = 50; \[Mu]0 = 5; \[Lambda]0 = 3;
(* Generate data *)
u = RandomReal[UniformDistribution[{0, 1}], n];
x = \[Mu]0 + Sqrt[Log[1 - u]/-\[Lambda]0];
(* Log likelihood *)
logL = n*Log[2] + n*Log[\[Lambda]] + \!\(
\*UnderoverscriptBox[\(\[Sum]\), \(i = 1\), \(n\)]\(Log[
x[\([i]\)] - \[Mu]]\)\) - \[Lambda]*\!\(
\*UnderoverscriptBox[\(\[Sum]\), \(i = 1\), \(n\)]
\*SuperscriptBox[\((x[\([i]\)] - \[Mu])\), \(2\)]\);
(* Find maximum likelihood estimates *)
sol = Maximize[{logL, \[Mu] < Min[x] && \[Lambda] >
0}, {\[Mu], \[Lambda]}]
mle = {\[Mu], \[Lambda]} /. sol[[2]];
(* First order partials *)
DlogL = D[logL, {{\[Mu], \[Lambda]}}];
(* Calculate variance estimates using second order partials *)
hessian = D[DlogL, {{\[Mu], \[Lambda]}}] /. sol[[2]];
v = -Inverse[hessian];
MatrixForm[v]
(* Check to see that the first order partials are close to zero with \
estimates of \[Mu] and \[Lambda] *)
DlogL /. sol[[2]]
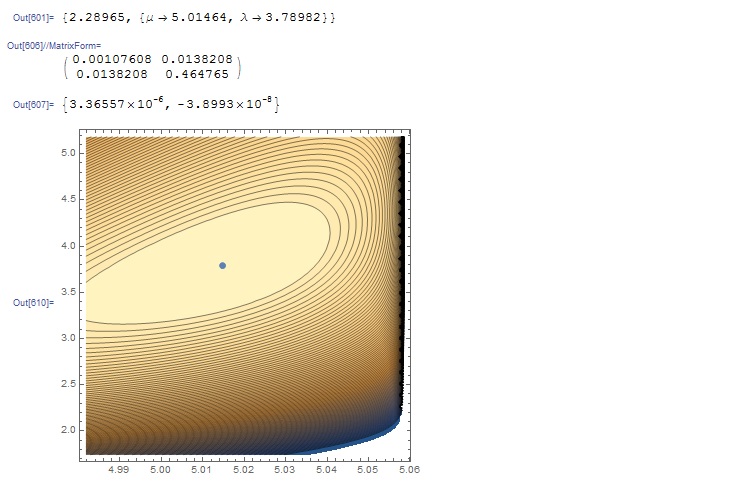
(* Additional check: show contour plot of log likelihood around the \
mle's *)
c = ContourPlot[logL, {\[Mu], mle[[1]] - v[[1, 1]]^0.5, Min[x]},
{\[Lambda], mle[[2]] - 3 v[[2, 2]]^0.5, mle[[2]] + 3 v[[2, 2]]},
Contours -> 100];
m = ListPlot[{mle}];
Show[{c, m}]
with the following output: