Thanks Nasser and Henrik
ok now I went to try the code for average with different values of constant c
data = Table[{i, [FT /. sol /. t -> i}, {i, -20, 20, .1}];
area = Integrate[x[t] /. sol, {t, -20, 20}];
average = area/(40);
with this code
Clear[t]
\[Tau] = 13.8;
r = 0.7071;
n = 1.7758;
\[Omega] = 0.5;
k = 1666666.667;
s = 2.2758;
cVals = {2.2758, 2.04822, 1.82064, 1.59306, 1.36548};
color = {Red, Yellow, Green, Cyan, Blue};
Do[c = cVals[[i]];
system1 = {x'[t] == n*y[t],
y'[t] == -n*x[t] - c*E^(-(r^2) - ((t^2*(1.177^2))/\[Tau]^2))*z[t],
z'[t] == c*E^(-(r^2) - ((t^2*(1.177^2))/\[Tau]^2))*y[t]};
initialvalues1 = {x[-20] == 0, y[-20] == 0, z[-20] == -1};
sol1 = NDSolve[
Join[system1, initialvalues1], {x[t], y[t], z[t]}, {t, -20, 20}];
F = -s*r*x[t]*E^(-(r^2) - ((t^2*(1.177^2))/\[Tau]^2));
FT = -c*r*y[t]*E^(-(r^2) - ((t^2*(1.177^2))/\[Tau]^2));
Subscript[plotF, i] =
Plot[Evaluate[F /. sol1], {t, -20, 20}, FrameLabel -> {"t", "F"},
Frame -> True, FrameTicks -> All, PlotStyle -> color[[i]]];
Subscript[plotFT, i] =
Plot[Evaluate[FT /. sol1], {t, -20, 20}, FrameLabel -> {"t", "FT"},
Frame -> True, FrameTicks -> All, PlotStyle -> color[[i]]];, {i,
Length[cVals]}]
Show[{Subscript[plotF, 1], Subscript[plotF, 2], Subscript[plotF, 3],
Subscript[plotF, 4], Subscript[plotF, 5]}]
Show[{Subscript[plotFT, 1], Subscript[plotFT, 2],
Subscript[plotFT, 3], Subscript[plotFT, 4], Subscript[plotFT, 5]}]
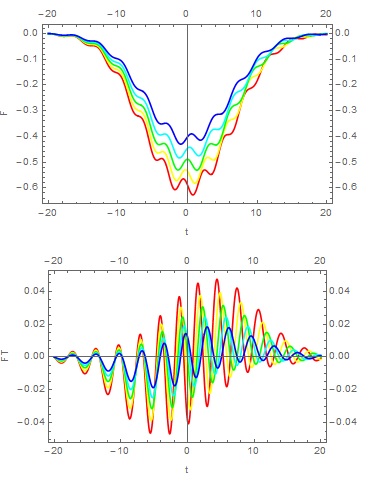
here in this code I have plot FT and F for different values of c (see the photo)
and what i want now is plot a variety of different graphs for the average F and FT over the range of c