Doesn't
In[13]:= Solve[Fold[1.02 #1 - #2 &, x, {500, 673, 245, 345, 245, 674, 425, 145, 37, 423}] == 0, x]
Out[13]= {{x -> 3378.77}}
help? (The interest is per year, the payment starts 6 month after the deposit and in the end no money remains.)
And this shows the account history just after a payment resp. the initial deposit
ListPlot[Transpose[
{Range[0, 5, 0.5], FoldList[1.02 #1 - #2 &, 3378.77, {500, 673, 245, 345, 245, 674, 425, 145, 37, 423}]}
], PlotLabel -> "Tim pays the bill"]
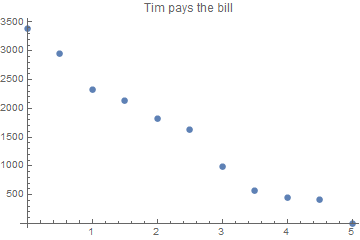
and this is what has been payed every half year:
In[32]:= (1.02 Most[#] - Rest[#])&[FoldList[1.02 #1 - #2 &, 3378.77, {500, 673, 245, 345, 245, 674, 425, 145, 37, 423}]]
Out[32]= {500., 673., 245., 345., 245., 674., 425., 145., 37., 423.}
probe it
In[33]:= % - {500, 673, 245, 345, 245, 674, 425, 145, 37, 423}
Out[33]= {0., 0., 0., 0., 0., 0., 0., 0., 0., 0.}