This problem is so interesting that I try a "solution" as well.
Let "img" be the original image. Then the trick can be done by:
imgLens =
Thinning@Binarize@
DeleteBorderComponents@
SelectComponents[Blur@EdgeDetect[img, 4],
"EnclosingComponentCount", # == 0 &]
which gives:

I am not really satisfied with this method, because it depends quite sensitive on the parameter of EdgeDetect.
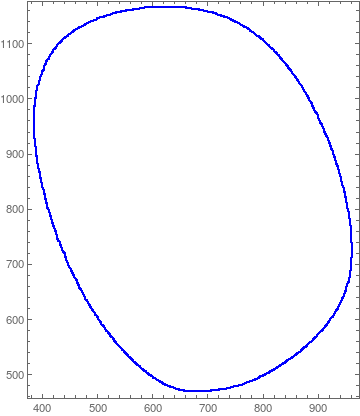
From this one can easily extract the coordinates of the boundary of the lens:
imgDims = ImageDimensions[imgLens];
pts = {#2, imgDims[[1]] - #1 + 1} & @@@
Position[ImageData@imgLens, 1, {2}];
Graphics[{Blue, PointSize[.004], Point[pts]}, Axes -> True,
Frame -> True]
Ciao Henrik