Message Boards Message Boards

0
|
9513 Views
|
6 Replies
|
4 Total Likes
View groups...
Share
Share this post:

Why does my fit not work?

Peter Parker, Research
Posted 9 years ago

Hey, I would like to fit my experimental results with the Airy function of a Fabry-Perot Etalon.

My data:

FresnelFit1={{1.549839`, 0.007287525118680326`}, {1.5498399999999999`, 
  0.00728592444798114`}, {1.549841`, 
  0.0072848405971469386`}, {1.549842`, 
  0.007284364374582154`}, {1.5498429999999999`, 
  0.0072845881201418616`}, {1.549844`, 
  0.007285601468836208`}, {1.549845`, 
  0.007287487259892552`}, {1.5498459999999998`, 
  0.007290317781755396`}, {1.549847`, 
  0.007294151518974972`}, {1.549848`, 
  0.007299030534781825`}, {1.549849`, 
  0.007304978585454492`}, {1.54985`, 
  0.007312000021581998`}, {1.5498509999999999`, 
  0.007320079489331453`}, {1.549852`, 
  0.007329182404157641`}, {1.549853`, 
  0.007339256132189752`}, {1.5498539999999998`, 
  0.007350231782686882`}, {1.549855`, 
  0.0073620264899909`}, {1.549856`, 
  0.007374546046404931`}, {1.549857`, 
  0.007387687738981427`}, {1.549858`, 
  0.007401343243399845`}, {1.5498589999999999`, 
  0.007415401436535378`}, {1.54986`, 
  0.007429751005089286`}, {1.549861`, 
  0.007444282749492882`}, {1.5498619999999999`, 
  0.007458891508621713`}, {1.549863`, 
  0.007473477659863467`}, {1.549864`, 
  0.0074879481788721015`}, {1.5498649999999998`, 
  0.007502217272028083`}, {1.549866`, 
  0.007516206620454852`}, {1.5498669999999999`, 
  0.007529845295892864`}, {1.549868`, 
  0.007543069424601624`}, {1.549869`, 
  0.007555821684932537`}, {1.5498699999999999`, 
  0.007568050726906313`}, {1.549871`, 
  0.007579710598101078`}, {1.549872`, 
  0.007590760249910437`}, {1.5498729999999998`, 
  0.007601163182663397`}, {1.549874`, 
  0.007610887268447398`}, {1.549875`, 
  0.0076199047682359395`}, {1.549876`, 
  0.007628192536747492`}, {1.549877`, 
  0.0076357323860610634`}, {1.5498779999999999`, 
  0.007642511559038358`}, {1.549879`, 
  0.007648523247544408`}, {1.54988`, 
  0.007653767079551442`}, {1.5498809999999998`, 
  0.007658249494350106`}, {1.549882`, 
  0.0076619839267752735`}, {1.549883`, 
  0.00766499072964343`}, {1.549884`, 
  0.007667296778114667`}, {1.549885`, 
  0.007668934719628011`}, {1.5498859999999999`, 
  0.007669941857226064`}, {1.549887`, 
  0.0076703586809820125`}, {1.549888`, 
  0.007670227090141663`}, {1.5498889999999999`, 
  0.007669588375646488`}, {1.54989`, 
  0.0076684810570517474`}, {1.549891`, 
  0.007666938687744237`}, {1.5498919999999998`, 
  0.007664987756260431`}, {1.549893`, 
  0.007662645818188556`}, {1.5498939999999999`, 
  0.007659919991788242`}, {1.549895`, 
  0.007656805940720709`}, {1.549896`, 
  0.007653287449290181`}, {1.5498969999999999`, 
  0.0076493366699958015`}, {1.549898`, 
  0.007644915091106534`}, {1.549899`, 
  0.007639975234953028`}, {1.5498999999999998`, 
  0.007634463057586709`}, {1.549901`, 
  0.0076283209795465065`}, {1.549902`, 
  0.0076214914379935704`}, {1.549903`, 
  0.0076139208147285335`}, {1.549904`, 
  0.007605563564776859`}, {1.5499049999999999`, 
  0.007596386348249003`}, {1.549906`, 
  0.007586371955620281`}, {1.549907`, 
  0.007575522814533699`}, {1.5499079999999998`, 
  0.007563863875269548`}, {1.549909`, 
  0.007551444692124907`}, {1.54991`, 
  0.007538340548477009`}, {1.549911`, 
  0.007524652513055391`}, {1.549912`, 
  0.007510506362171391`}, {1.5499129999999999`, 
  0.007496050355147937`}, {1.549914`, 
  0.00748145190540724`}, {1.549915`, 
  0.007466893244839003`}, {1.5499159999999998`, 
  0.007452566231340248`}, {1.549917`, 
  0.007438666496015945`}, {1.549918`, 
  0.007425387164906448`}, {1.5499189999999998`, 
  0.007412912418075339`}, {1.54992`, 
  0.007401411164748084`}, {1.5499209999999999`, 
  0.007391031115824304`}, {1.549922`, 
  0.007381893524037558`}, {1.549923`, 
  0.007374088837545597`}, {1.5499239999999999`, 
  0.007367673475735633`}, {1.549925`, 
  0.007362667888118727`}, {1.549926`, 
  0.0073590560005493705`}, {1.5499269999999998`, 
  0.00735678609031113`}, {1.549928`, 
  0.007355773065882151`}, {1.549929`, 
  0.007355902061665628`}, {1.54993`, 0.007357033195909293`}};

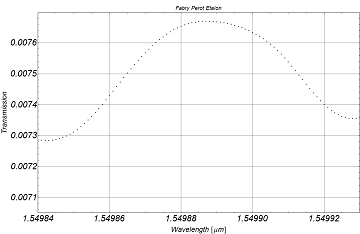
enter image description here

My equation is: 

n=1.46;
L=0.001002;

model = ((1 - r1^2)*(1 - r2^2))/((1 - r1*r2)^2 + 
        4*r1*r2 (Sin[(((2 \[Pi] 10^6)/\[Lambda]) 2 n L  Cos[\[Theta]])/
           2])^2) *I0;

r1 und r2: reflection coefficient for mirrors

n: refraction index

Theta: angle of incident light

Lambda: wavelength

L: length of the etalon

I0: Intensity of incoming beam

Here comes my fit:

nlm = NonlinearModelFit[FresnelFit1, model, {
   {r1, 0.20},
   {r2, 0.20},
   {I0, 0.0077},
   {\[Theta], 2.0}},
  \[Lambda], MaxIterations -> 50001] ;

fit = nlm["BestFitParameters"]      

modelf = Normal[nlm]

After evaluation of the code, you will see, that the fitted parameter make absolutly no sense. I dont understand this, because the choosen start values are very close to the true values as it can be seen in the next plot, where I use excatly these start values and compare it with the experimental data (dashed line):

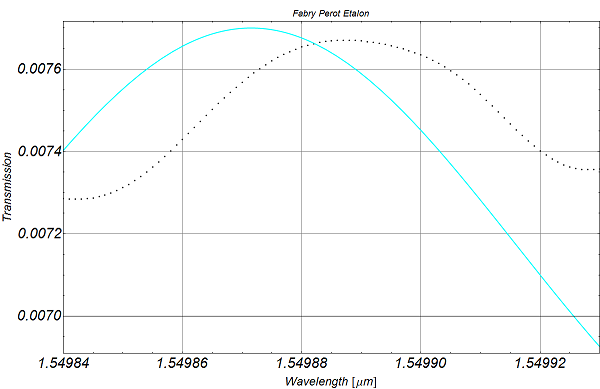
enter image description here

Can somebody tell me what I am doing wrong? Why can Mathematica not fit the experimental curve with this equation?
POSTED BY: Peter Parker
6 Replies
Sort By:
Jason Zhao
Jason Zhao, GEICO
Posted 4 years ago

5 years past, there's still no GAM model built in.
POSTED BY: Jason Zhao

Hi Peter,

I cannot see any problem:

n = 1.46; L = 0.001002;

model = ((1 - r1^2)*(1 - r2^2))/((1 - r1*r2)^2 + 
      4*r1*r2 (Sin[(((2 \[Pi] 10^6)/(\[Lambda])) 2 n L Cos[\[Theta]])/
           2])^2)*I0;

nlm = NonlinearModelFit[FresnelFit1, 
   model, {{r1, 0.30}, {r2, 0.30}, {I0, 0.0077}, {\[Theta], 
     2.0}}, \[Lambda], MaxIterations -> Automatic];

Show[ListLinePlot[FresnelFit1, PlotStyle -> {Green, Dashed}],
 Plot[nlm[\[Lambda]], {\[Lambda], 1.549, 1.55}]]

which gives:

enter image description here

Well, I slightly changed the initial values of the r's and the number of MaxIterations, but that does not make a significant difference.

Tschau! ... Henrik
POSTED BY: Henrik Schachner
Jim Baldwin
Jim Baldwin, Retired
Posted 9 years ago

As Henrik shows, Mathematica is performing properly.

However, you really need to consider a better model or additional data. If "prediction" is the most important objective, then using ListInterpolation (in this case where there is so little variability about the line) works great:

f = ListInterpolation[FresnelFit1[[All, 2]], {FresnelFit1[[All, 1]]}];
Show[{ListPlot[FresnelFit1, Frame -> True, 
   PlotRange -> {Automatic, {0.0071, 0.0077}}, 
   PlotStyle -> {Red, PointSize[0.01]}], 
  Plot[f[\[Lambda]], {\[Lambda], Min[FresnelFit1[[All, 1]]], 
    Max[FresnelFit1[[All, 1]]]}, PlotStyle -> Blue]}, 
 ImageSize -> Large]

model fit

For noisier data a nonparametric fit (such as a gam - generalized additive model) would be better. However, Mathematica as far as I know does not supply a gam function or other nonparametric fits (Developers: Please!).

If interpretation of the coefficients is a more important objective, then you need a different model as there is a not a good fit and there's no point in interpreting coefficients or providing estimates of coefficients of a poorly fitting model. Something must be missing in the model or in how the data is actually generated.

My experience is in fields were large amounts of variability is the expected norm. If I saw such data in one of those fields, I would wonder if all of the observations are highly serially correlated and in such a case the NonlinearModelFit is inappropriate as it does not allow for serial correlation. Is the data from a single run of some measurement process? If so, I'd say you have a sample size of one and would need replication of the measurement process to fight off the claim (at least potentially) that the model as presented is not a good fit. But here, too, with multiple sets of measurements, NonlinearModelFit does not handle mixed models (i.e., where there is more than one source of variability: between sets of measurements and serial correlation). Adding mixed models to Mathematica's repertoire would also be great.
POSTED BY: Jim Baldwin

Oh sorry, seems that I forgot to mention that

n=1.46; L=0.001002;

I also added this information to my first post.

Furthermore I think by copy and paste the numbers of my list, the value (last digits) changed. This is why your ListPlot does not look like my ListPlot in the first post. Therefore I also changed this in my first post. If you plot the data now, they should look like in my first figure.

Yes, the equation should be correct. I checked it and it makes sense.
POSTED BY: Peter Parker
Jim Baldwin
Jim Baldwin, Retired
Posted 9 years ago

Sorry. Forgot to add something. I'm not familiar with this particular curve form. Is there really a cosine inside of the sine as the model indicates?
POSTED BY: Jim Baldwin
Jim Baldwin
Jim Baldwin, Retired
Posted 9 years ago

It looks like the constants n and L are missing from your example code. And the plot of the data doesn't look like a perfect fit to the dashed line:

ListPlot[FresnelFit1, Frame -> True]

produces

scatter plot
POSTED BY: Jim Baldwin
Reply to this discussion
Community posts can be styled and formatted using the Markdown syntax.
Tag limit exceeded
Note: Only the first five people you tag will receive an email notification; the other tagged names will appear as links to their profiles.
Reply Preview
Attachments
Remove
or Discard

Group Abstract Group Abstract