Are you sure that that is the correct function?
Each of the three terms is non-negative:
Show[Plot[1/Sqrt[x^2 + 1], {x, -5, 5}, PlotRange -> {All, {0, 2}}], Plot[Cosh[x], {x, -5, 5}], Plot[x^2, {x, -5, 5}]]
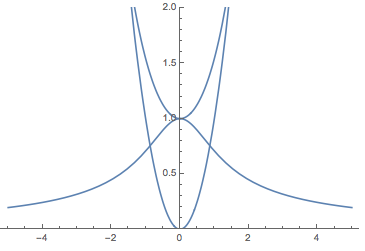
One of them is always larger or equal one. (In fact apart from x=0 all three terms are always positive. At x=0 the sum is 2.) So I would expect the sum to be always larger than 0. Hence there are no real zeros. When t=0 the Cosh is one for all x. For t>0, Cos[t x]>=1, so t does not help here.
Cheers,
M.