Group Abstract Group Abstract

Message Boards Message Boards

0
|
8.7K Views
|
7 Replies
|
7 Total Likes
View groups...
Share
Share this post:

MLE: NMaximize vs FindDistributionParameters

Sandu Ursu
Posted 11 years ago

2 simple ways to perform (simple) Maximum Likelihood Estimation in Mathematica:

(1) Construct the Log-Likelihood function and maximize it:

enter image description here

(2) Define the Probability Distribution and find parameters:

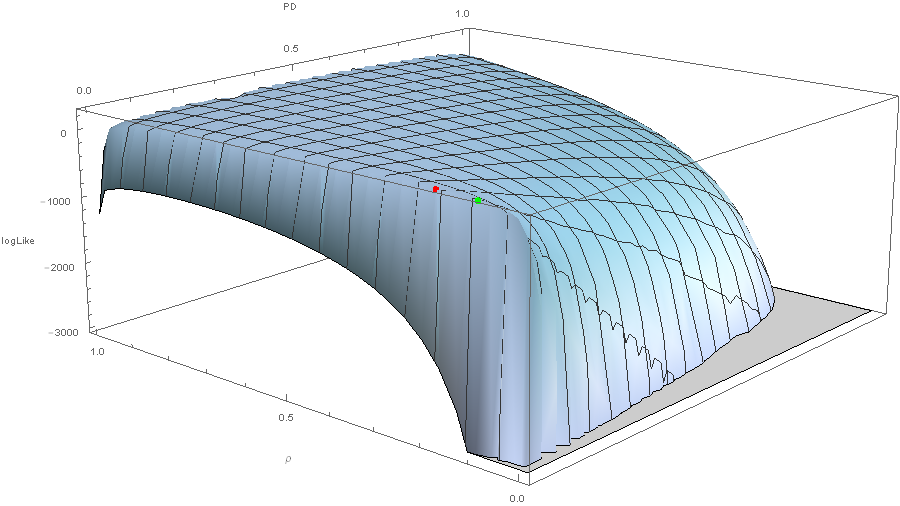
enter image description here

They are not that much different, in the sense that they yield close values for the Log-Likelihood function (shown in the plot below), but still, the difference is noticeable in the resulting values of the parameters and I am curious which should I trust more?

enter image description here

Attachments:
POSTED BY: Sandu Ursu
7 Replies
Sort By:
Jim Baldwin
Jim Baldwin, Retired
Posted 11 years ago

Thanks, Marco. Usually the Hessian (or an approximation of it) is created during the iterative process for finding maximum likelihood estimates so I would think that it shouldn't be too much trouble to make that available (or its inverse when it exists) as an option for FindDistributionParameters.

If Wolfram is packaging these high level functions to be of value other than being a good way to obtain starting values for a more detailed analysis, I would consider that providing these estimated standard errors is essential.

Jim
POSTED BY: Jim Baldwin
Jim Baldwin
Jim Baldwin, Retired
Posted 11 years ago

Maybe it's part of the documentation and I just don't see it but it appears for FindDistributionParameters, there is no option to obtain estimates of the standard errors and covariances of the parameter estimators. A Statistics golden rule is "An estimate without an associated estimate of precision is at best of unknown value."

Bruce Miller: Where do I send such suggestions?
POSTED BY: Jim Baldwin

See also:

http://mathematica.stackexchange.com/questions/6498/standard-errors-for-maximum-likelihood-estimates-in-finddistributionparameters

and

http://community.wolfram.com/groups/-/m/t/201528

Cheers,

M.
POSTED BY: Marco Thiel

Jim,
Suggestions can be sent via http://www.wolfram.com/support/contact/email/?topic=Technical

A simple code example with actual output and preferred output would help clarify the issue.

POSTED BY: Bruce Miller
Jim Baldwin
Jim Baldwin, Retired
Posted 11 years ago

I continue to make more than my fair share of programming mistakes (especially with Mathematica). The only ways I know how to minimize such occurrences are to (1) perform lots of checks (Do the probability functions sum/integrate to 1 for arbitrary parameters?), and (2) (probably the best technique) Grab anybody and explain your problem with the code in front of both of you. Then either that person will catch the obvious (upper/lowercase, spelling, etc.) or while you're explaining you'll say "Oh, nevermind." because the issue will become obvious.
POSTED BY: Jim Baldwin
Jim Baldwin
Jim Baldwin, Retired
Posted 11 years ago

The two solutions are too far apart to be considered similar. The issue is that a factor of 1/2 is missing from the pdf definition. To match the likelihood the pdf needs to be

pdf[x_] := 
  Sqrt[(1 - \[Rho])/\[Rho]]
    Exp[(inN[x]^2 - ((Sqrt[1 - \[Rho]] inN[x] - inN[PD])/
        Sqrt[\[Rho]])^2)/2];

Now the result will be 

{PD -> 0.013438593418697627473, \[Rho] -> 0.10995316859509961784}

which matches 

{137.731, {PD -> 0.0134386, \[Rho] -> 0.109953}}
POSTED BY: Jim Baldwin
Sandu Ursu
Sandu Ursu
Posted 11 years ago

That's embarrassing..

Thank you, Jim!
POSTED BY: Sandu Ursu
Reply to this discussion
Community posts can be styled and formatted using the Markdown syntax.
Tag limit exceeded
Note: Only the first five people you tag will receive an email notification; the other tagged names will appear as links to their profiles.
Reply Preview
Attachments
Remove
or Discard