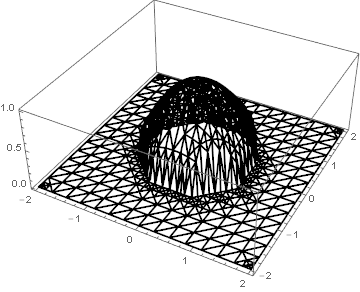
f[x_, y_] := If[x^2 + y^2 > 1, h = 0, h = (Cos[(y \[Pi])/2] Cos[(x \[Pi])/2])^0.5];
Plot3D[f[x, y], {x, 2, -2}, {y, 2, -2}]
Extracting them may be complicated because those intersections are not calculated. Mesh lines are done for each direction separately.
But you can easily create them by yourself:
Array[{##, f[##]} &, {17, 17}, {{-2, 2}, {-2, 2}}]
Graphics3D[ Point /@ % ]
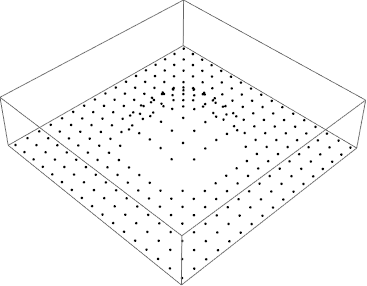
On the other hand you can extract actual plot polygons verices:
Plot3D[{If[x^2 + y^2 > 1, h = 0,
h = (Cos[(y \[Pi])/2] Cos[(x \[Pi])/2])^0.5]}, {x, 2, -2}, {y,
2, -2}, Mesh -> None,
PlotStyle -> Directive[EdgeForm[Thick], FaceForm@None]
]
% // Cases[#, GraphicsComplex[pts_, ___] :> pts] & // Short
{{{-2.,-2.,0.}, <<562>>,{<<1>>}}}
Or use V10 fancy stuff:
DiscretizeGraphics @ First @ Normal @ Plot3D[ f[x,y], {x, 2, -2}, {y, 2, -2}, Mesh -> None]
MeshCoordinates@% // Shallow
 {{-1.85714,-1.85714,0.},{-1.71429,-2.,0.},{-1.71429,-1.71429,0.},{0.,-1.71429,0.},{-0.285714,-2.,0.},{0.,-2.,0.},{-1.42857,-1.71429,0.},{-1.42857,-2.,0.},{-1.14286,-1.71429,0.},{-1.14286,-2.,0.},<<554>>}
{{-1.85714,-1.85714,0.},{-1.71429,-2.,0.},{-1.71429,-1.71429,0.},{0.,-1.71429,0.},{-0.285714,-2.,0.},{0.,-2.,0.},{-1.42857,-1.71429,0.},{-1.42857,-2.,0.},{-1.14286,-1.71429,0.},{-1.14286,-2.,0.},<<554>>}