Hi guys, using a code like this:
Table[{{i, j, k, l}}, {i,1,2}, {j,1,2}, {k,1,2}, {l,1,2}] // MatrixForm
I obtain a nested list:
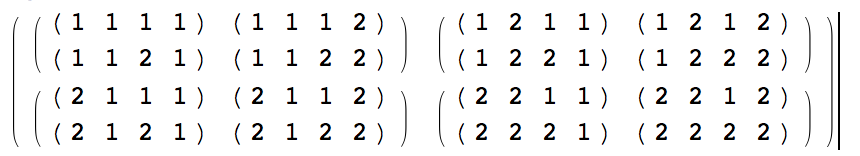
Instead of that, I'd like to obtain just a simple array composed of 16 vectors 1x4 like this one:
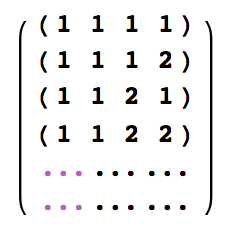
I need that because i have to do those calculations:
vectors =
Table[KroneckerProduct[misure[[i]], misure[[j]], misure[[k]],
misure[[l]]], {i, 1, 2}, {j, 1, 2}, {k, 1, 2}, {l, 1, 2}];
aspectedvalue =
Table[FullSimplify[
Abs[KroneckerProduct[misure[[i]], misure[[j]], misure[[k]],
misure[[l]]].ConjugateTranspose[\[Psi]]]^2,
Assumptions -> {\[Phi] \[Element] Reals}], {i, 1, 2}, {j, 1,
2}, {k, 1, 2}, {l, 1, 2}];
and I want to obtain a simple output in both.
In the first one, I'd like to obtain a 16x(1x16) array of vectors (misure[[i]] are 1x2 vectors, and the kronecker product of 4 of them gives a 1x16 vector); in the latter I'd like to obtain a 16x1 vector (because those are just scalars.). If there isn't a clever way to do this with table, I'll use for cycles...
I hope I made myself clear, thank you