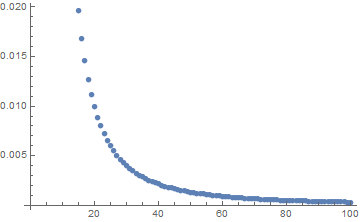
I know you want to solve this in Wolfram Alpha but all I can offer is one way to do it in Mathematica:
solutions = p /. Table[Flatten[N[Solve[Sum[Binomial[n, k]*p^k*(1 - p)^(n - k), {k, 3, n/2}] == Sum[p^k*(1 - p)^(n - k)*(Binomial[n, k] - Binomial[n/2, k]*2^k), {k, 2, n/2}] &&
0 < p < 1, p, Reals]]], {n, 6, 100}]
ListPlot[Table[{n, solutions[[n - 5]]}, {n, 6, 100}]]
with output
{0.272727, 0.166667, 0.105573, 0.074773, 0.0556628, 0.0430781, \
0.0343294, 0.0280016, 0.0232764, 0.0196548, 0.0168176, 0.0145537, \
0.0127181, 0.0112094, 0.0099541, 0.00889856, 0.00800249, 0.00723531, \
0.00657342, 0.0059984, 0.00549568, 0.00505362, 0.00466285, \
0.00431572, 0.00400596, 0.00372841, 0.00347873, 0.00325332, \
0.00304914, 0.0028636, 0.00269449, 0.00253993, 0.0023983, 0.0022682, \
0.00214841, 0.00203786, 0.00193563, 0.0018409, 0.00175297, \
0.00167118, 0.00159499, 0.0015239, 0.00145745, 0.00139526, \
0.00133697, 0.00128225, 0.00123083, 0.00118244, 0.00113684, \
0.00109384, 0.00105323, 0.00101484, 0.00097851, 0.000944098, \
0.00091147, 0.000880505, 0.000851092, 0.000823128, 0.00079652, \
0.000771181, 0.000747033, 0.000724002, 0.00070202, 0.000681023, \
0.000660955, 0.000641761, 0.000623391, 0.000605799, 0.000588941, \
0.000572778, 0.00055727, 0.000542384, 0.000528087, 0.000514347, \
0.000501137, 0.000488429, 0.000476199, 0.000464422, 0.000453077, \
0.000442143, 0.0004316, 0.000421429, 0.000411614, 0.000402137, \
0.000392985, 0.000384141, 0.000375592, 0.000367326, 0.000359329, \
0.000351591, 0.0003441, 0.000336846, 0.000329819, 0.00032301, \
0.000316409}