Alas, the REAL $\pi$ day of the century -- the only one that most of us currently living will ever see -- is over.

But don't despair! There are other $\pi$'s, in fact infinitely many, and they have been tragically ignored in favor of the so-called REAL $\pi$. These other $\pi$'s happen to be formal power series, so there should be a number of perfectly legitimate FORMAL POWER SERIES $\pi$ days of the century, and we can't possibly have missed them all, right?

Since at least the 1930s, people have been interested in formal power series analogues of real numbers. A real number like $\pi$ is an infinite sum of powers of $10$, each multiplied by a coefficient:

$$\pi = 3 \cdot \frac{1}{10^0} + 1 \cdot \frac{1}{10^1} + 4 \cdot \frac{1}{10^2} + 1 \cdot \frac{1}{10^3} + 5 \cdot \frac{1}{10^4} + \cdots$$

If we replace $10$ with $x$, then we get a formal power series. We choose a prime $p$, and the allowable coefficients are $0, 1, \dots, p - 1$. The difference is that when we add or multiply power series, we use arithmetic modulo $p$ for the coefficients.

Well, in this "number system" of formal power series modulo $p$, there is a "number" that plays an analogous role to the real number $\pi$. It's defined as an infinite product. Here are the first few terms in the expansion of the $p = 2$ analogue, $\pi_2$:

In[1]:= With[{p = 2}, MapAt[Mod[#, p] &, Series[Product[1 - (x^p^n - x)/(x^p^(n + 1) - x), {n, 1, 5}], {x, Infinity, 20}], 3]]
    %[[3]]

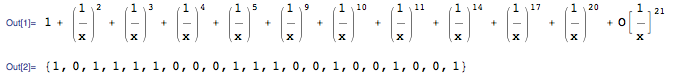
In a 1935 paper, Leonard Carlitz defined formal power series analogues of the exponential function, the logarithm, and even the Riemann zeta function. The remarkable fact is that the special power series $\pi_p$ is related to those functions in ways that parallel the familiar properties of their counterparts, for example the exponential function being periodic with period $2 \pi i$, and the fact that the Riemann zeta function evaluated at $2 m$ is a rational number times $\pi^{2m}$. It's also known that $\pi_p$ is transcendental, just like $\pi$, but over the field of rational power series rather than the field of rational numbers.

So there we go! The $\pi_2$ day of the century was 1/01/11 -- January 1st, 2011. Huh, I guess we already missed that one...

What about $\pi_p$ for other primes $p$?

In[3]:= With[{p = 3}, MapAt[Mod[#, p] &, Series[Product[1 - (x^p^n - x)/(x^p^(n + 1) - x), {n, 1, 5}], {x, Infinity, 20}], 3]]
    %[[3]]

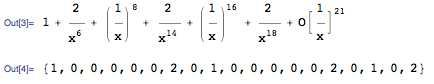
In[5]:= With[{p = 5}, MapAt[Mod[#, p] &, Series[Product[1 - (x^p^n - x)/(x^p^(n + 1) - x), {n, 1, 5}], {x, Infinity, 20}], 3]]
    %[[3]]

Nope; the nonzero terms are too sparse to extract a meaningful date! Unfortunately, this problem will probably just get worse as we increase $p$. So maybe we need to look elsewhere for analogues of $\pi$ that contain good dates in their expansions. But on the bright side, you only have to wait 96 years instead of a full century for the next big $\pi$ day.