Both Wolfram Alpha and Mathematica suggest that there is a finite area between the intersections.
fx = -0.00000086 x^4 + 0.00012 x^3 - 0.00466 x^2 + 0.1463 x - 12.18156;
gx = -0.000000000005 x^6 - 0.000000004 x^5 + 0.0000009 x^4 - 0.0001 x^3 + 0.0078 x^2 - 0.3838 x + 13.299
We can calculate the intersections:
intersecs = NSolve[{fx == gx, x \[Element] Reals}, x]
(*{{x -> -1143.28}, {x -> 167.48}}*)
We can now integrate:
Integrate[gx - fx, {x, x /. intersecs[[1]], x /. intersecs[[2]]}]
(*4.53217*10^8*)
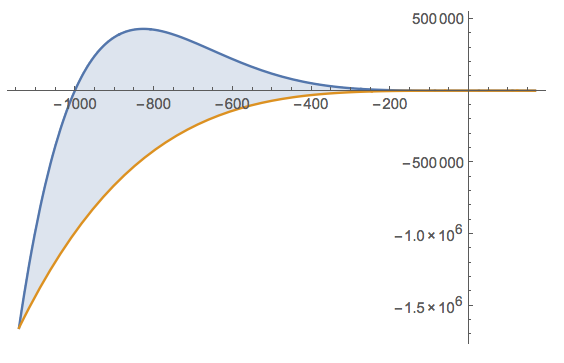
Here is the plot that looks just like the one that Wolfram Alpha produces:
Plot[{gx, fx}, {x, x /. intersecs[[1]], x /. intersecs[[2]]}, Filling -> { 1 -> {2}}, PlotRange -> All]
Cheers,
Marco