Given i^(2/7), I get the following result:
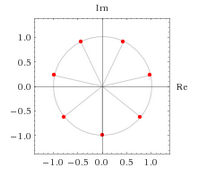
Which doesn't look correct to me. So, I entered "7th root of -1", which gave me this:
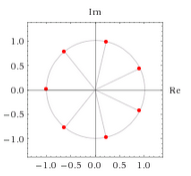
Which is what I expected. So I thought, perhaps these aren't equivalent and I've gone wrong somewhere? I entered "(7th root of -1) = i^(2/7)":
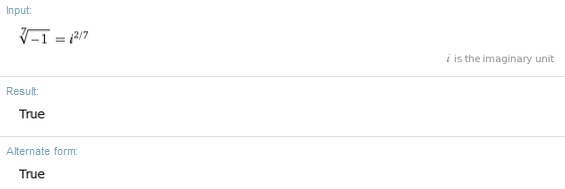
WolframAlpha appears to be contradicting itself! Looking more closely, the two seem to be rotations of one another.
Is this a bug, or am I missing something here?
Links
Equality

Imaginary power

7th root of -1
