I don't know if this qualifies for your first case but this is how a three dimensional space could be set up in GrassmannCalculus. The following declares a 3-dimensional point space with coordinates x, y and z, and establishes it with a vector basis. The other choice is an exterior form basis. This also establishes a, b, c, d and subscripted g's as scalar symbols in the system. The symbols p, q, r and s are established as symbolic vector symbols. A Grassmann point space is one that has an origin as well as free vectors. You can declare spaces with and without an origin and with and without a metric. (The FivePointedStar character doesn't display nicely in a posting. )
You now have a space with all the facilities of Grassmann algebra built in.
<< GrassmannCalculus`
SetGrassmannNSpace[3, {x, y, z}, "Vector"]
\[FivePointedStar]S[a, b, c, d, Subscript[g, _, _]];
\[FivePointedStar]V[p, q, r, s]
The following shows a basis palette that is established for all grades of the algebra. These are buttons that will paste to the notebook.
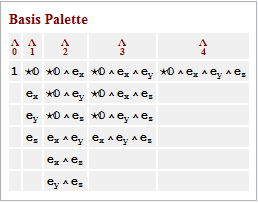
You can switch to a form basis with:
SwitchBasis["Form"]
The new Basis palette is:
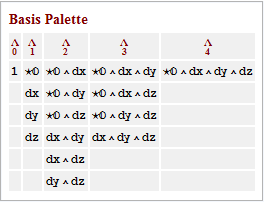
The following declares a specific symbolic metric.
DeclareMetric[
DiagonalMatrix[{Subscript[g, 1, 1], Subscript[g, 2, 2], Subscript[g,
3, 3]}]]
The following is the metric palette that shows the induced metrics associated with each sub-algebra of various grades.

The following is a palette with Mathematica Rules for exterior products.

These are rules for Regressive products. Again, these can be pasted into a notebook.

These Rules are built into most of the symbolic operations, but they do give some ability to do detailed manipulation.
I hope this is some help. It does give a taste for what can be done with Mathematica. John Browne's book on Grassmann Algebra is available at: Grassmann Algebra Book
I'm currently implementing the use of Mathematica 10 Associations. These are quite nice because everything is retrieved by keys and the particular order of things in the Association is not important. So a user could create an Association for his particular problem that contained the core data for Grassmann algebra, but then add other items such as charts for a manifold and transition functions between them - or whatever pertained to the particular project.