Thank you for your reply. However, I have already experimented with Theorema, and while its ultimate goal might be to handle cases like mine, it is nowhere to close to that right now. At this moment, it does not even have axioms for set theory built in, let alone metric spaces, tensors and integrals.

Yes, it certainly seems to be. I was aware of it, but just wanted to confirm (by asking this question) that the kind of things I'm trying to do are indeed the ones Wolfram states (in the blog entry) that Mathematica cannot presently do.

In that case, my question is: is there any add-on to Mathematica, or an entirely different system (Magma, maybe?) which CAN do things like this? Theorema (mentioned above) might aspire to this end, but is in a very early stage of development, and not helpful to me as of now.

Here is the direct quote:

"In the calculational case, one’s typically dealing with an operation to be performed. In the Wolfram|Alpha-like pure mathematical case, one’s typically just giving a description of something. In some cases that description will be explicit. A specific number. A particular equation. A specific graph. But more often it will be implicit. It will be a set of constraints. One will say (to use the example from above), “Let F be a field,” and then one will give constraints that the field must satisfy.

But to really be useful in pure mathematics, there’s something else that’s needed. In addition to being able to deal with concrete mathematical objects, one also has to be able to deal with abstract mathematical structures. Countless pure mathematical papers start with things like, “Let F be a field with such-and-such properties.” We need to be able to enter something like this—then have our system automatically give us interesting facts and theorems about F, in effect creating a whole automatically generated paper that tells the story of F.

So what would be involved in creating a system to do this? Is it even possible? There are several different components, all quite difficult and time consuming to build. But based on my experiences with Mathematica, Wolfram|Alpha, and A New Kind of Science, I am quite certain that with the right leadership and enough effort, all of them can in fact be built."

Consider the exact example he gives of something Mathematica cannot represent - "Let F be a field with such-and-such properties". Consider the first axiom I have in my original post - "M3 is a metric space with a metric tensor g". From the point of view of level of abstraction, they seem to be similar.

Your example shows that theorem proving in possible using simple propositional calculus and first-order logic constructs. This is well known to me. However, my question is whether Mathematica can provide a True/False answer (which is a strictly weaker requirement than actually proving that answer. I would love to have a proof, but at this point I don't expect it) to statements involving abstract mathematical structures like fields. A first order logic statement does not involve abstract mathematical structures. From the above quotation, Wolfram's answer appears to be that this is not possible at present.

It seems that True/False answers involving arithmetic are possible. I was able to ask Mathematica if the square root of 2 is rational, and it replied with False, although I don't believe a proof can be generated at present. Theorema (an add-on package for Mathematica) should eventually be able to provide proofs of things like this, but cannot at present.

I would LOVE to be proved wrong. In fact, I posted this question hoping that I'll be proved wrong. But that would involve someone providing a Wolfram Language translation of say, the first axiom I provide. If someone knows of an add-on or different algebra system (Magma?) that makes this possible, I'd be delighted as well.

I don't know if this qualifies for your first case but this is how a three dimensional space could be set up in GrassmannCalculus. The following declares a 3-dimensional point space with coordinates x, y and z, and establishes it with a vector basis. The other choice is an exterior form basis. This also establishes a, b, c, d and subscripted g's as scalar symbols in the system. The symbols p, q, r and s are established as symbolic vector symbols. A Grassmann point space is one that has an origin as well as free vectors. You can declare spaces with and without an origin and with and without a metric. (The FivePointedStar character doesn't display nicely in a posting. )

You now have a space with all the facilities of Grassmann algebra built in.

<< GrassmannCalculus`
SetGrassmannNSpace[3, {x, y, z}, "Vector"]
\[FivePointedStar]S[a, b, c, d, Subscript[g, _, _]];
\[FivePointedStar]V[p, q, r, s]

The following shows a basis palette that is established for all grades of the algebra. These are buttons that will paste to the notebook.

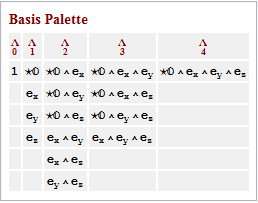
You can switch to a form basis with:

SwitchBasis["Form"]

The new Basis palette is:

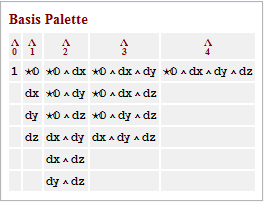
The following declares a specific symbolic metric.

DeclareMetric[
 DiagonalMatrix[{Subscript[g, 1, 1], Subscript[g, 2, 2], Subscript[g, 
   3, 3]}]]

The following is the metric palette that shows the induced metrics associated with each sub-algebra of various grades.

The following is a palette with Mathematica Rules for exterior products.

These are rules for Regressive products. Again, these can be pasted into a notebook.

These Rules are built into most of the symbolic operations, but they do give some ability to do detailed manipulation.

I hope this is some help. It does give a taste for what can be done with Mathematica. John Browne's book on Grassmann Algebra is available at: Grassmann Algebra Book I'm currently implementing the use of Mathematica 10 Associations. These are quite nice because everything is retrieved by keys and the particular order of things in the Association is not important. So a user could create an Association for his particular problem that contained the core data for Grassmann algebra, but then add other items such as charts for a manifold and transition functions between them - or whatever pertained to the particular project.

Although I'm not sure if anything here applies to my case, it does seem to be a case of abstract mathematics represented in Mathematica. I will look into it further.

Thank you very much for taking the time to answer!

I have. I understand that it's partly a theorem prover. From what I understand, theorem provers can, in principle, prove (or try to prove, given limited time resources) any theorem in mathematics, no matter how abstract, since all of mathematics is apparently reducible to FOL. In practice, however, this would require thousands of axioms, and impossible amounts of time for any non-trivial theorem.

That's why it may be beneficial for a theorem prover to integrate/communicate with Mathematica. However, no such link exists with Coq. The only theorem prover I know of which does integrate with modern versions of Mathematica is Theorema 2, which is in too early a stage of development to be useful for non-trivial proofs. (There's also Analytica, which is old, and doesn't work on Mathematica versions after 4 or so.)