There is a Button on the site Reddit, which resets a sixty second countdown. As long as the countdown never finishes, the button remains.

The site's users, of which there are more than three million, may each press the button once. Since April 1st, they have pressed the button nearly one million times, perpetuating it for more than a month and a half.

Each user permanently bears the time they reset the countdown from; users compete, compare, and argue over pushing at various times. In the beginning times less than 50s were impossible, whilst today almost a third of times are single digit. Users are also colour coded into tens (and thus teams), 50's are purple, single digits red.

This has produced some awesome visualisations, and a host of difficult questions, spanning game theory, community psychology, and statistics.

A keen Mathematica user, I felt I could bring more visualisations (and some analysis) to the table

I start by bringing a large raw data set (April 3rd to May 20th, available here) into Mathematica, and finding the times where the timer increases (implying it has been reset.)

Data = Import["C:\\Users\\Me\\Desktop\\button.csv"];
Positives = First /@ Position[Sign[Differences[Data[[2 ;;, 2]]]], 1];

Then I cut the data into lists of reset times for each hour. For each hour (as a rolling average), the odds that each second will be reset (once begun) are calculated. I graph these in tens: single digits have red axes, tens, twenties, thirties, forties, and fifties, orange, yellow, green, blue and purple respectively. Within each graph Red is the first number (eg 59) and blue the last (eg 52). Thus each graph describes the population growth of each coloured team, and its devaluation as increasing proportions move through to the next colour. X axis hours since April 3rd.

Hours = (Data[[2 ;;, 3]] /. {0 -> 60}) & /@ (GatherBy[Positives, Ceiling[#/3600] &]); 
Volumes = BinCounts[#, {0, 60, 1}] & /@ Hours;
Passrates = Table[Quiet[Prepend[1 - (Volumes[[i]][[#]]/Total[Volumes[[i]][[1 ;; #]]] // N) & /@ Range[2, 60], 0]] /. Indeterminate -> 0, {i, Length[Volumes]}];
temp = Transpose[MovingAverage[Passrates, 24]];
Partition[Table[ListPlot[temp[[10 a + 1 ;; 10 a + 10]], PlotRange -> All, Joined -> True, PlotStyle -> "TemperatureMap", ImageSize -> Medium, AxesStyle -> {Purple, Blue, Green, Yellow, Orange, Red}[[6 - a]]], {a, 5, 0, -1}], 3] // Grid

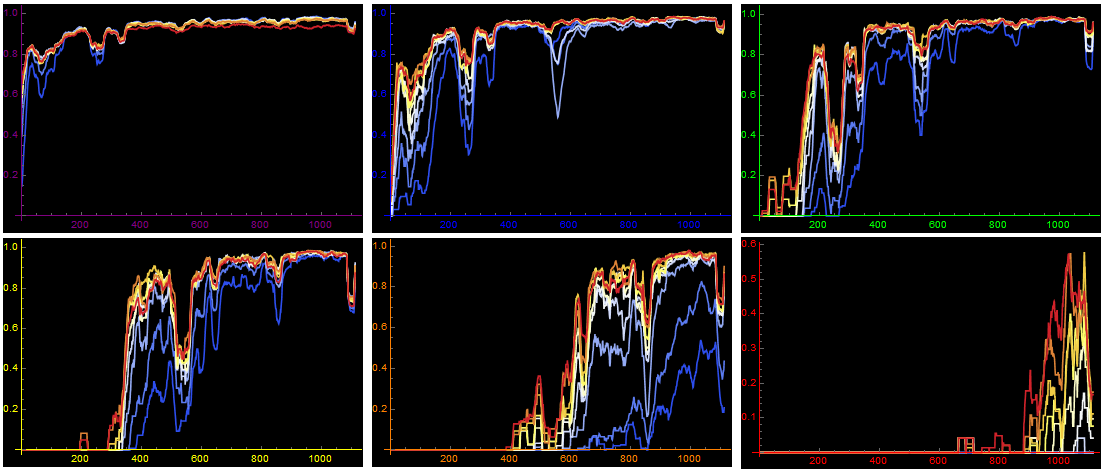
Viewing the data all at once, four or five distinct cliffs can be seen, where people are prompt to select the rarer colours from low timers. As these numbers become more commonplace, the distinctions reduce.

ListPointPlot3D[MovingAverage[SecondPassrates, 24]]

I wanted to find a simple formulation for this noisy ongoing change. I conjecture that peoples choices are primarily dependent on current rarity: at first a 40 was rare, and thus contested, as more 40's are taken, the value ascribed to a 40 decreases, and so lower numbers are reached. To this end I took the hourly volumes for each number and calculated log rarity (log 1 / probability of event) for each second, and plot against the observed rarity. This measure of the value of 'being ahead' proves extremely consistent!

PassingProportion = #/Total[#] & /@ 
   N[MovingAverage[BinCounts[#, {0, 60, 1}] & /@ Hours, 24]];
tempdat = 
  Drop[#, 1] & /@ Table[{Total[First /@ #], #[[1, 2]], i} & /@  SplitBy[Transpose[{PassingProportion[[i]],
         -Log[1 - (Total[PassingProportion[[i]][[# ;; -1]]] & /@ Range[60])]}], Last], {i, Length[PassingProportion]}] /.
   {Indeterminate -> 0, ComplexInfinity -> 0, 52 - 4 I -> 56};
ListPointPlot3D[tempdat, ColorFunction -> "TemperatureMap",  Background -> Black, BoxRatios -> {1, 1, 1}, ImagePadding -> 50]

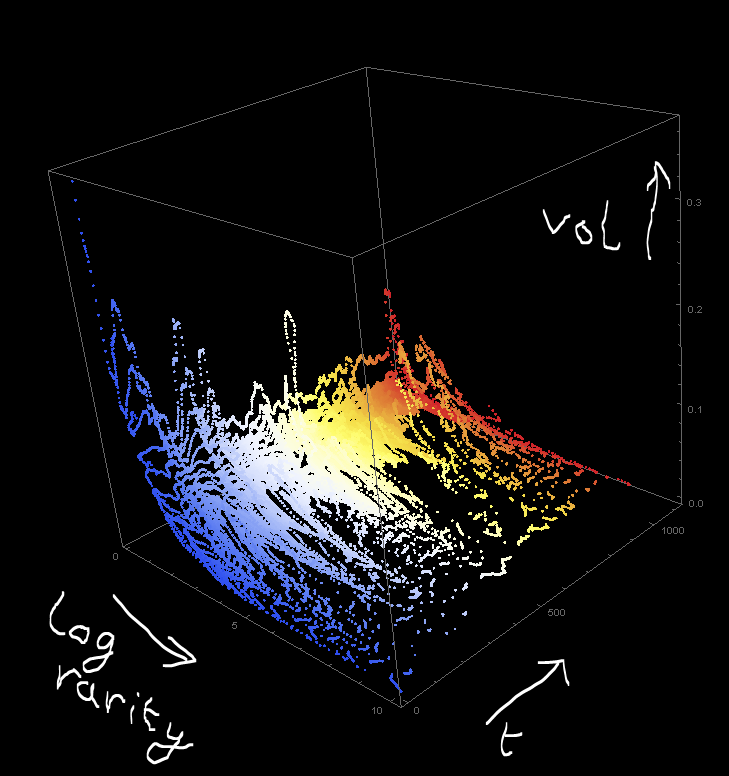
Nonlinear model fitting quickly reduces this to an equation with only one time dependent term. This fudge factor likely contains various disregarded elements such as people with specific numeric targets.

TimeFunction[t_] := E^(-0.0052123 t)
LogCoefficient[t_] := 0.0634394 + 0.3266820 TimeFunction[t]
LogLogCoefficient[t_] := -0.1382703 - 0.8857738 TimeFunction[t]
AppealDistribution[x_, t_] := -0.0104844 + LogCoefficient[t] Log[1 + 1 x] + LogLogCoefficient[t] Log[Log[2 + 1 x]]
Plot3D[AppealDistribution[x, t], {x, 0, 16}, {t, 0, 1100}, PlotRange -> {0, 0.35}, BoxRatios -> {1, 1, 1}]

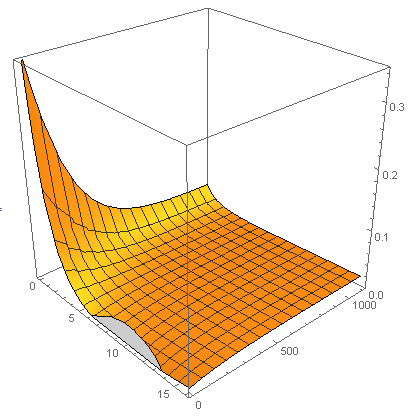
The parameterisation allows prediction of future number proportions from current ones, whilst simply defined and a nice average, the model is too simple for any long term predictions. Pictured, the transition from the end of the data to my projection:

Suffice to say Reddit has come up with a unique experiment!

I'm told nice clean server side data will be published when the button finally ends.

Moderation Team Note: We think you meant this link to Button - is it right? The one in your post below returns "page not found".