For this type of non-linear equation, best to use FindRoot as follows:
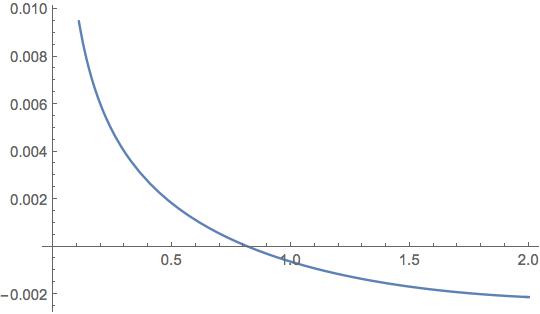
In[22]:= FindRoot[eq, {p, 1.}]
Out[22]= {p -> 0.81974}
In[25]:= Plot[Evaluate[eq[[1]]], {p, 0, 2}]
The solution is also apparent from the plot:
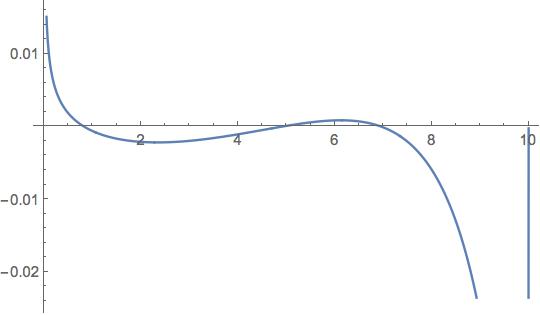
More roots can be found:
In[30]:= eq = (E^(-2 Sqrt[
20 - 2 p]) (-2 Sqrt[-(-10 + p) p] Sin[
Sqrt[2] Sqrt[p]]^2 - (-10 + p) Sin[2 Sqrt[2] Sqrt[p]]))/
p == 0;
In[31]:= FindRoot[Evaluate[eq], {p, 6}]
Out[31]= {p -> 4.9348}
In[32]:= FindRoot[Evaluate[eq], {p, 7.}]
Out[32]= {p -> 6.94577}