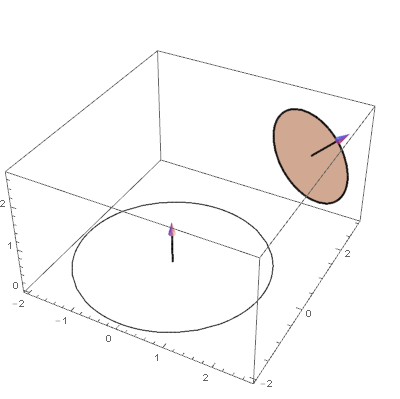
The Presentations Application sold through my web site had Circle3D and Disk3D routines. These date back to about Mathematica 6 but still are convenient. One specifies the location, orientation and radius along with possible options.
<< Presentations`
$PlotTheme = "Classic";
Draw3DItems[
{Opacity[0.8],
{FaceForm[Lighter@Brown],
Disk3D[{2, 2, 2}, {2, 0, 2}, 1, Mesh -> None],
Thick,
Circle3D[{2, 2, 2}, {2, 0, 2}, 1]},
Circle3D[{0, 0, 0}, {0, 0, 1}, 2],
Arrow3D[{0, 0, 0}, {0, 0, 1}, {0.3}],
Arrow3D[{2, 2, 2}, {2, 2, 2} + Normalize[{2, 0, 2}], {0.3}]},
NeutralLighting[0, 0.5, 0.1],
NiceRotation,
PlotRange -> All,
Axes -> True,
ImageSize -> 400]