I think there are two issues you might consider: (1) Explicitly assign the results of NDSolve rather than using a reference (%21) and (2) I think one needs to "create" the derivatives from the results of NDSolve. Here's a modification of your code:
\[Kappa]2 = 0.04745;
\[Kappa]1 = 0.002832;
\[Epsilon] = 0.01;
sol = Flatten[
NDSolve[{u1a''[x] == 2 \[Kappa]2^2 (u1a[x] - u2b[x]),
u2b''[x] == 2 \[Kappa]2^2 (u2b[x] - u1a[x]),
u4a''[x] == 2 \[Kappa]2^2 (u4a[x] - u6b[x]),
u6b''[x] == 2 \[Kappa]2^2 (u6b[x] - u4a[x]),
u4b''[x] == 2 \[Kappa]2^2 (u4b[x] - u2a[x]),
u2a''[x] == 2 \[Kappa]2^2 (u2a[x] - u4b[x]), u1a[0] == 0,
u2b'[0] == 0, u4a[1] == u4b[1],
u2a'[1] == \[Kappa]1 (u6b[1] - u2a[1]),
u6b'[1] == \[Kappa]1 (u6b[1] - u2a[1]), u4b'[1] == u4a'[1],
u1a'[1/2] == \[Kappa]1 (u4b[1/2] - u1a[1/2]),
u4b'[1/2] == \[Kappa]1 (u4b[1/2] - u1a[1/2]),
u2a'[1/2] == u2b'[1/2], u2a[1/2] == u2b[1/2],
u6b[3/2] == 3 \[Epsilon]/2, u4a[3/2] == 3 \[Epsilon]/2}, {u1a[x],
u2b[x], u4a[x], u6b[x], u4b[x], u2a[x]}, {x, 0, 3/2}]]
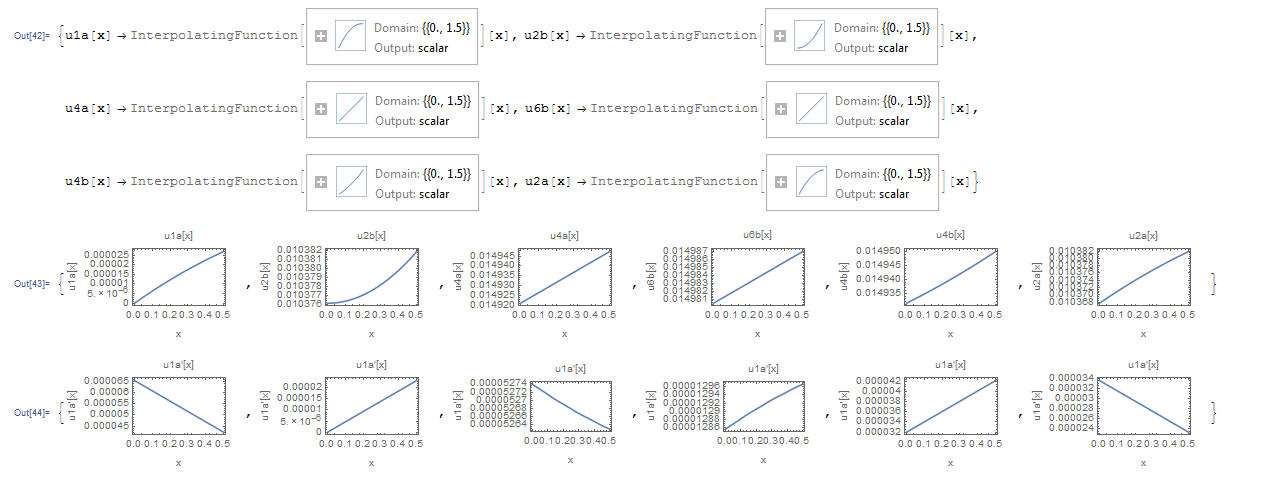
Table[Plot[(sol[[i]] /. x -> y)[[2]], {y, 0, 1/2}, Frame -> True,
FrameLabel -> {{ToString[sol[[i, 1]]], ""}, {"x", ToString[sol[[i, 1]]]}}], {i, 6}]
Table[Plot[(D[sol[[i]], x] /. x -> y)[[2]], {y, 0, 1/2}, Frame -> True,
FrameLabel -> {{ToString[D[sol[[1, 1]], x]], ""}, {"x", ToString[D[sol[[1, 1]], x]]}}], {i, 6}]