This is one of my first times using Mathematica;
... and you have choosen as starting point the modification of a demonstration using the ShowLabeledGraph, HasseDiagram, MakeGraph functions from the Combinatorica package. That's hard because it presumes the understanding of all that stuff. A modest beginning on your own
Clear[s2v, zevHasseD]
s2v[n_Integer?Positive, l_List] := 1 /; Length[l] == 0
s2v[n_Integer?Positive, l_List] :=
2^n /; Length[l] == n (* Sort[l] \[Equal] Range[n] *)
s2v[n_Integer?Positive, l_List] :=
Sum[Binomial[n, o], {o, 0, Length[l] - 1}] +
Position[Subsets[Range[n], {Length[l]}], l][[1, 1]] /;
0 < Length[l] < n
zevHasseD[n_Integer?Positive, zev_List] :=
Module[{pS, zevS, gR, gV, gC, gH},
If[n > 10,
Print["The power set of Range[", n, "] has ", 2^n,
" members. Try a smaller number n, please."];
Return[$Failed], (* else, pS[[1]] is the empty set *)
pS = Subsets[Range[n], {#}]& /@ Range[0, n]
];
gR = Join[UndirectedEdge[1, #]& /@ Range[2, n + 1],
Flatten[
Table[UndirectedEdge[s2v[n, #[[1]]], s2v[n, #[[2]]]] & /@
Select[Flatten[Outer[List, pS[[o]], pS[[o + 1]], 1], 1],
Intersection @@ # == First[#] &], {o, 2, n}], 1]];
gV = Rule[s2v[n, #], ToString[#]] & /@ Flatten[pS, 1];
gC = Join[{{0, 0}},
Flatten[Table[{oo - Ceiling[Length[pS[[o]]]/2], o - 1}, {o, 2,
n + 1}, {oo, 1, Length[pS[[o]]]}], 1]];
zevS = Flatten[pS, 1] \[Intersection] (Sort /@ zev);
If[Length[zevS] == 0,
Print["Set zev has empty intersection with the power set of ",
Range[n], ". Just drawing it's Hasse diagram."];
(* Hasse *)
Graph[gR, VertexLabels -> gV, VertexCoordinates -> gC], (* else *)
Print["Sets to mark up: ", zevS, ". Draw an augmented Hasse diagram."];
(* Hasse augmented *)
gH = s2v[n, #]& /@ zevS;
Graph[gR, VertexLabels -> gV, VertexCoordinates -> gC, GraphHighlight -> gH]
]
] /; VectorQ[zev, VectorQ]
had brought you some modest success
zevHasseD[5, {{1, 5}, {1, 3, 4}, {1, 5, 3, 4}, {2, 3}, {3, 4, 5}, {2, 3, 6}}]
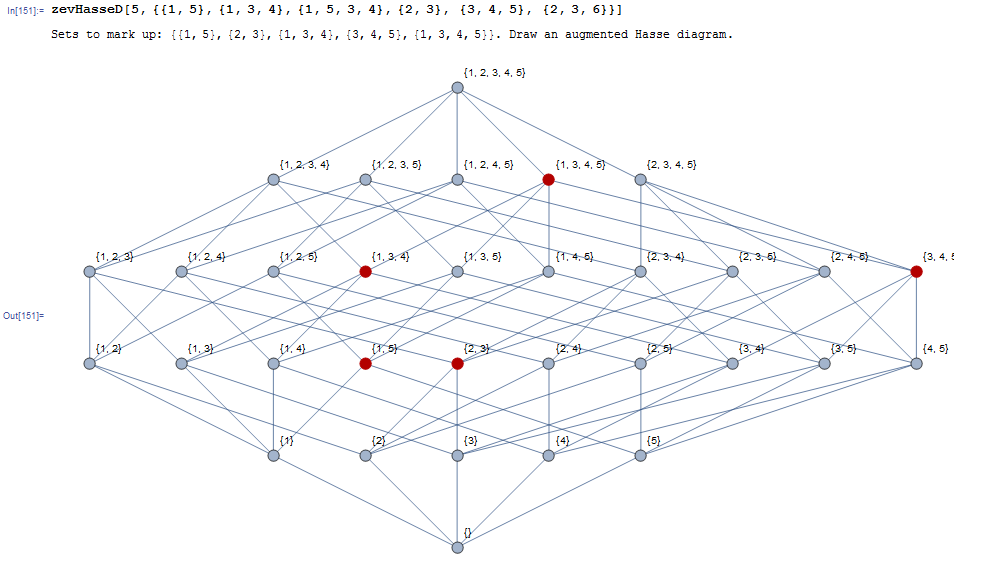
using this you might
edit the EdgeColor section of the code to EdgeStyle with a simple
pattern
by taking advantage of the GraphHighlight above, which is able to highlight edges too. Such edges must be only selected from the above gR. Later on you can put everything into a Manipulate to generate a nice looking augmented Hasse Diagram Viewer.