I don't have answer for the general density of this probability density (and it might not even have a compact form) but for the specific parameters you use one can obtain a nonparametric density estimate as good as you like by using a large enough sample size:
\[Omega] = 2.7;
\[Mu]P = 700;
\[Sigma]P = 200;
\[Mu]EP = 800;
\[Sigma]EP = 200;
x1 = RandomVariate[NormalDistribution[\[Mu]P, \[Sigma]P], 1000];
x2 = RandomVariate[NormalDistribution[\[Mu]EP, \[Sigma]EP], 1000];
q = x1 (1 - (1 + (x2/x1) - (1 + (x2/x1)^\[Omega])^(1/\[Omega])));
Plot[PDF[SmoothKernelDistribution[q], x], {x, 0, 1000}]
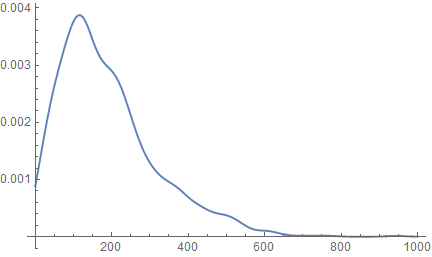
But with some samples and almost certainly with large samples, you will have issues when either x1 or x2 is negative unless Abs[x2/x1] is used (although that is likely not the variable of interest).