The equation of the sphere is easy:

\[Rho] == 2

The equation of the cylinder is:

\[Rho] == 2 Cos[\[Phi]] Csc[\[Theta]]

See SphericalPlot3D for information about rho, theta, and phi. Theta and phi can change from one text to another.

Here is a plot:

SphericalPlot3D[{{2}, {2 Cos[\[Phi]] Csc[\[Theta]]}}, {\[Theta], 0, 
  Pi}, {\[Phi], 0, 2 Pi}]

Eric

This is the 3D contour plot of exactly the author's equations: {x^2 + y^2 + z^2 == 4, x^2 + y^2 - 2 x == 0}

ContourPlot3D[{x^2 + y^2 + z^2 == 4, x^2 + y^2 - 2 x == 0}, {x, -2, 
  2}, {y, -2, 2}, {z, -2, 2}, AxesOrigin -> {0, 0, 0}, 
 AxesStyle -> Thick]

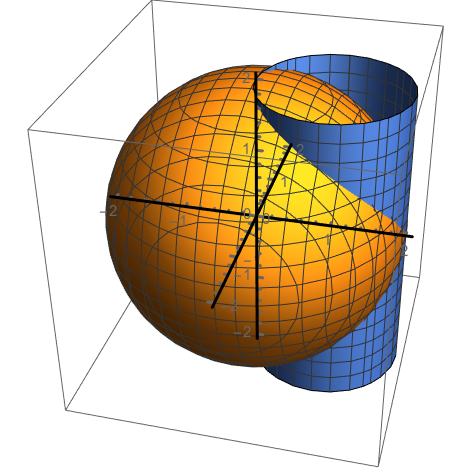
Which gives the above plot!

To calculate the volume, you have to use solids equivalent to those equations:

Graphics3D[{Ball[{0, 0, 0}, 2], Cylinder[{{1, 0, -2}, {1, 0, 2}}, 1]},
  Axes -> True]

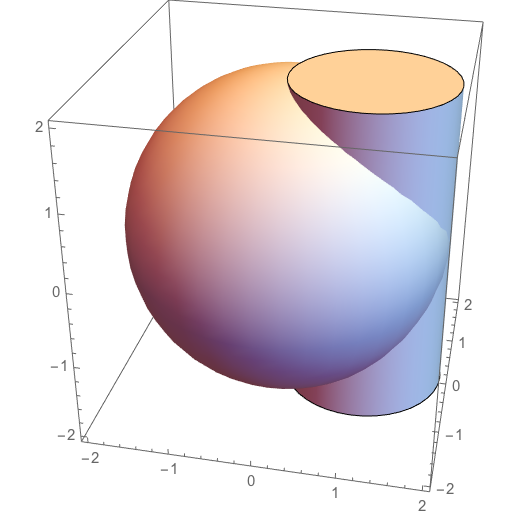
Which is different from Simon's plot due to the centre of the sphere not being the author's The volumes of the ball, the cylinder and their intersection can be perfectly calculated with Mathematica as I did in my first answer:

In[101]:= R1 = Ball[{0, 0, 0}, 2];
R2 = Cylinder[{{1, 0, -2}, {1, 0, 2}}, 1];
R = RegionIntersection[R1, R2];
Volume /@ {R1, R2, R}

Out[104]= {(32 \[Pi])/3, 4 \[Pi], 16/9 (-4 + 3 \[Pi])}

The above is not the correct plot of the two volumes of subject. The centre of the sphere is at {0,0,0} i.o at (0,01/2}. As can be seen from this plot:

Use the geometric computation functions:

In[27]:= R1 = Ball[{0, 0, 0}, 2];
R2 = Cylinder[{{1, 0, -2}, {1, 0, 2}}, 1];
R = RegionIntersection[R1, R2];

In[32]:= RegionMeasure@R

Out[32]= 16/9 (-4 + 3 \[Pi])