There is indeed a problem (or bug?) here:
Take the manipulate:
Manipulate[
Column[{RegionMeasure[r3[c]],
Graphics[{EdgeForm[Black], FaceForm[Gray], r1, EdgeForm[Red],
FaceForm[], r2[c]}, Axes -> True,
PlotRange -> {{-25, 25}, {-2, 7}}, ImageSize -> Medium]}], {{c,
2.5}, -.50, 6}]

If you move the c slider toward c <=2, one start getting the error
RegionMeasure::reg: r3[1.38] is not a correctly specified region. >>
or worse, the kernel quit (exited) with the "why the beep?" message: "The kernel Local has quit (exited) during the course of this evaluation". And you lose all previous function definitions...
However, I succeeded in making the plot:
ListLinePlot@Table[{c, Area[r3[c]]}, {c, 0, 4, .25}]
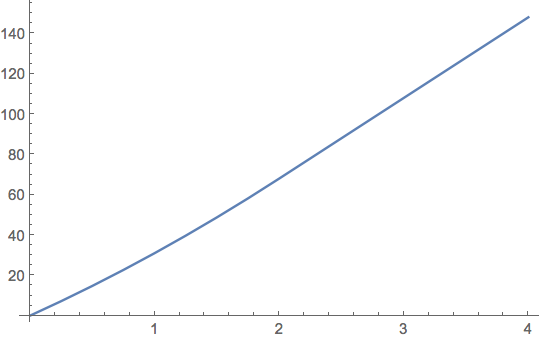
But any change in the plotting or table limits will give the" kernel exited" beep.
This error or bug, with only a beep and the" kernel exited" message is typical for v10. on OS X10.10? I get this a lot of times using e.g. ParametricPlot3D. never got anything like this before.