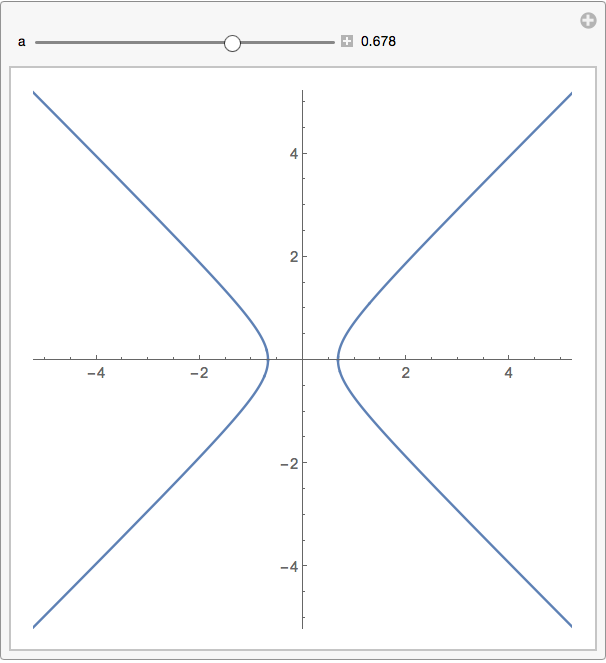
Take x^2-y+2=a and later make a go to zero
In[13]:= x^2 - y^2 == a /.
Thread[Rule[{x, y}, FromPolarCoordinates[{r, \[Theta]}]]];
Solve[%, r]
Out[14]= {{r -> -(Sqrt[a]/Sqrt[
Cos[\[Theta]]^2 - Sin[\[Theta]]^2])}, {r -> Sqrt[a]/Sqrt[
Cos[\[Theta]]^2 - Sin[\[Theta]]^2]}}
You can see a approach zero in this manipulate:
Manipulate[
PolarPlot[a/Sqrt[
Cos[\[Theta]]^2 - Sin[\[Theta]]^2], {\[Theta], 0, 2 \[Pi]},
PlotPoints -> 1000, PlotRange -> 5], {{a, 0.5}, 0.02, 1,
Appearance -> "Labeled"}]