First ask yourself, how would I do this with a paper and pencil. Then you'll know what steps to take in Mathematica.

The first step is to use Implicit differentiation to find the value of y'. You can do that in Mathematica with:

D[x^2 + y[x]^2 == c y[x], x]

Solve[%, y'[x]]

{y'[x] -> (2 x)/(c - 2 y[x])}

The value orthogonal to this is -1/y'[x].

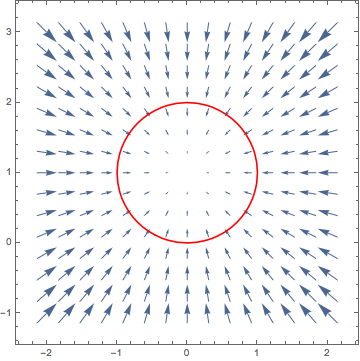
We can visualize the results:

cPlot = ContourPlot[x^2 + y^2 == 2 y, {x, -2, 2}, {y, -1, 3}, ContourStyle -> Red]

vPlot = VectorPlot[{-2 x, 2 - 2 y}, {x, -2, 2}, {y, -1, 3}]

Show[vPlot, cPlot]