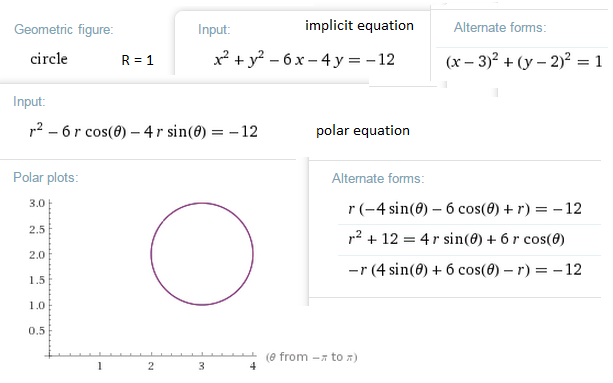
In[1]:= r^2 - 6 r Cos[\[Theta]] - 4 r Sin[\[Theta]] == -12
Out[1]= r^2 - 6 r Cos[\[Theta]] - 4 r Sin[\[Theta]] == -12
In[2]:= Solve[r^2 - 6 r Cos[\[Theta]] - 4 r Sin[\[Theta]] == -12, r]
Out[2]= {{r ->
1/2 (6 Cos[\[Theta]] + 4 Sin[\[Theta]] -
Sqrt[2] Sqrt[-11 + 5 Cos[2 \[Theta]] +
12 Sin[2 \[Theta]]])}, {r ->
1/2 (6 Cos[\[Theta]] + 4 Sin[\[Theta]] +
Sqrt[2] Sqrt[-11 + 5 Cos[2 \[Theta]] + 12 Sin[2 \[Theta]]])}}
In[5]:= PolarPlot[
1/2 (6 Cos[\[Theta]] + 4 Sin[\[Theta]] -
Sqrt[2] Sqrt[-11 + 5 Cos[2 \[Theta]] +
12 Sin[2 \[Theta]]]), {\[Theta], 0, 2 Pi}]