We stumbled upon this nearly 20 years old (according to author) web page titled Wie man mit 10 Bällen jongliert which in German means "How to juggle 10 balls". With the kind permission of the author Felix Holderied I am reproducing here the code and animation slightly changed. Enjoy ;-)

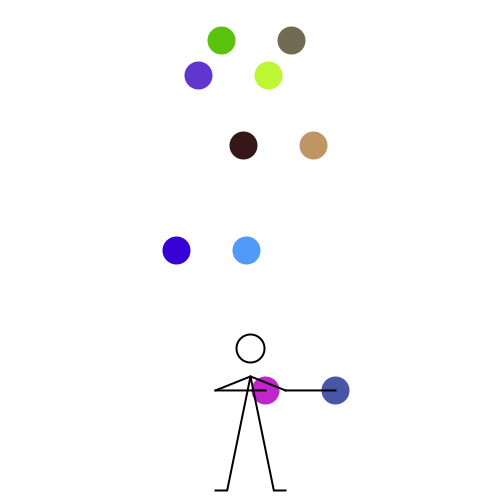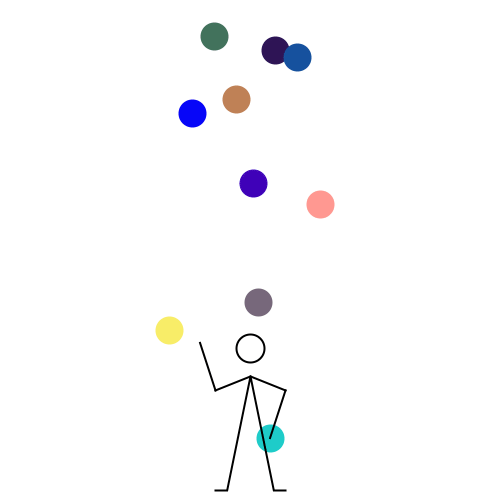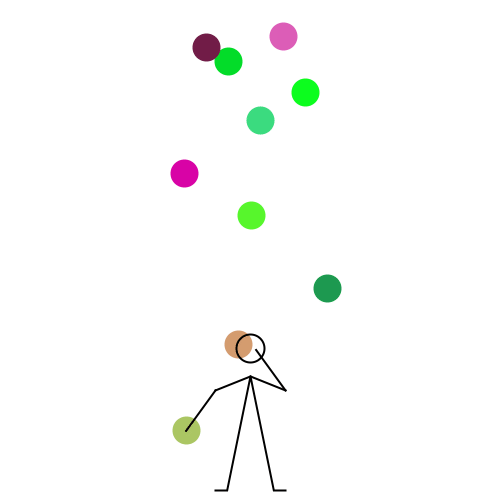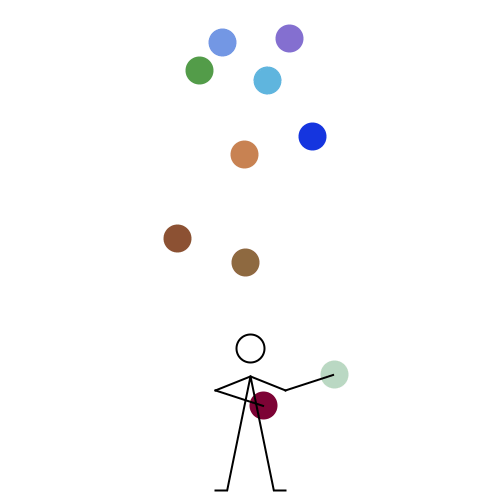
n = 5;
T = 1;
b = 20;
tw = t /. 
   FindRoot[
    1 == Pi/T Tan[2 Pi t/T] ((2 n - 1)/2 T - 2 t), {t, 0.9 T/4}];
r = 5 ((2 n - 1)/2 T - 2 tw) T/(2 Pi Cos[2 Pi tw/T]) // N;

SHL[t_] := r {Cos[2 Pi t/T], Sin[2 Pi t/T]} // N;
SHR[t_] := {-1, 1} SHL[t + T/2];
VH[t_] := r {-2 Pi Sin[(2*Pi*t)/T]/T, 2 Pi Cos[(2 Pi t)/T]/T} // N;
SB[t_] := SHL[tw] + VH[tw] (t - tw) - {0, 5 (t - tw)^2} // N;

hw = SHL[tw][[2]];
h = VH[tw][[2]]^2/20 + hw;
la = n/2;

jglr = ParallelTable[

  Bll = Table[If[SB[t + (b - 1) T][[2]] > hw,
     {RandomColor[], Disk[SB[t + (b - 1) T] - {la, 0}, 1]},
     {RandomColor[], Disk[SHL[t] - {la, 0}, 1]}], {b, n}];

  Blr = Table[
    If[SB[t + (b - 1.5) T][[2]] > hw, {RandomColor[], 
      Disk[{-1, 1} SB[t + (b - 1.5) T] + {la, 0}, 1]}, {RandomColor[],
       Disk[SHR[t] + {la, 0}, 1]}], {b, n}];

  Show[Graphics[{
     Bll, Blr,
     Thick,
     Line[{{la, 0}, SHR[t] - {-la, 0}}],
     Line[{{-la, 0}, SHL[t] - {la, 0}}],
     Line[{{la, 0}, {0, 1}}],
     Line[{{-la, 0}, {0, 1}}],
     Circle[{0, 3}, 1],
     Line[{{-la, -2 r}, {-2/3 la, -2 r}, {0, 
        1}, {2/3 la, -2 r}, {la, -2 r}}]}], 
   PlotRange -> 1.1 {{-(h + 2 r)/2, (h + 2 r)/2}, {-2 r, h}}], {t, 0, 
   T (1 - 1/b), T/b}]

Export["jglr.gif", jglr, ImageSize -> 500]