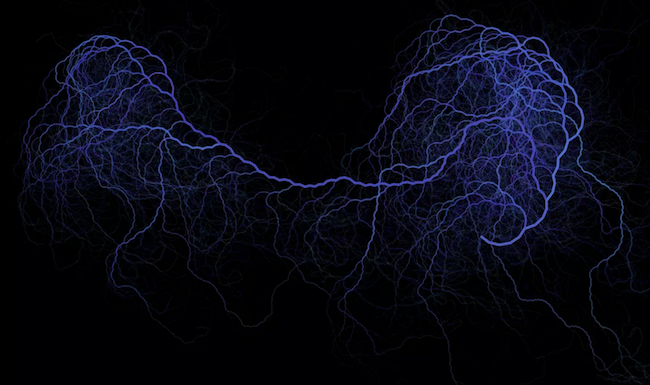
We've run into this interesting Reddit discussion using Wolfram Language (WL). This maybe interesting to folks curious about Collatz conjecture (see NKS Book page 904 ) or new in WL AnglePath function ( also see relevant Curlicue Fractals post ). Quoting the original post:

What a little playing with Mathematica can lead to:

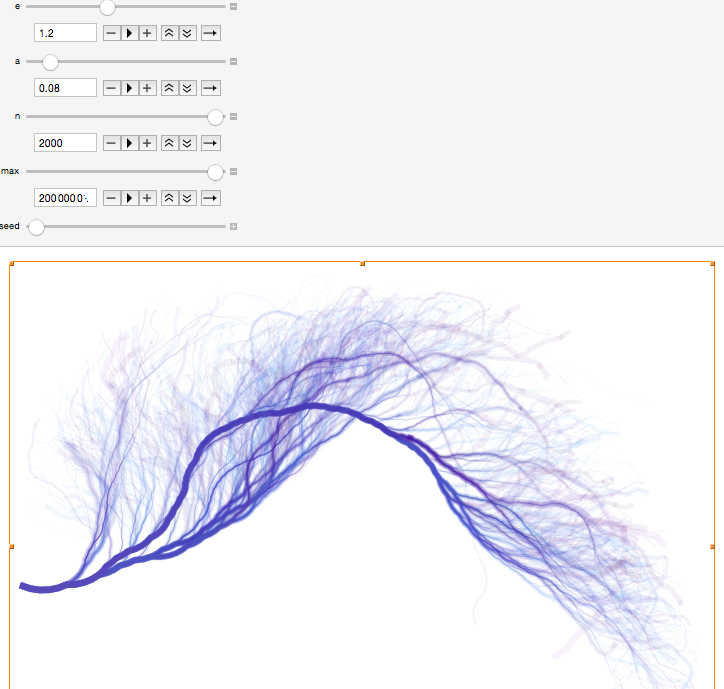
This is basically a procedure which takes n=2000 random numbers up to max=200000000, calculates the Collatz sequence for each of them and then turns each sequence into a curve using the AnglePath command: starting with 1, if the current number is even, it turns counterclockwise and if odd, it turns clockwise (the numbers in these sequences are mostly even, so I had to balance out the angles a bit so that on average the trajectories don't turn into a big spiral), and the length of the step decreases like a power of the number (1.2 in the picture). You can see that some paths repeat many times and most of the sequences at some point coalesce with one of these "thick" paths. More over, most (if not all) of the smaller paths approach the thicker paths from a particular side (I wonder what that means).

GITHUB: https://github.com/level1807/collatz.git

By going to the above GitHub link you can find relevant Wolfram Language code, for instance this will make a Manipulate similar to one in the picture:

<< ExampleData/Collatz.m;

Manipulate[seed;
 Graphics[{ColorData["SunsetColors"][RandomReal[]], 
     Thickness[0.0001 + 0.003 ((max - #)/max)^(4 e)], 
     Opacity[0.05 + 0.5 (#/max)^3], 
     Line[AnglePath[
       Table[{r/(1 + r^e), a Pi (Log[2]/Log[6] - Mod[r, 2])}, {r, 
         Reverse@Collatz[#]}]]]} & /@ 
   Reverse[Sort@RandomSample[Range[max], n]], Background -> Black, 
  ImageSize -> 800], {{e, 1.2}, 0.01, 3}, {{a, 0.34}, 0, 
  1}, {{n, 200}, 1, 2000, 1}, {{max, 200000000}, n, 200000000}, {seed,0, 1}, 
TrackedSymbols :> {n, max, seed, e, a}]

P.S. Other images that was created and posted on that Reddit thread: